За последнее десятилетие были разработаны и успешно применяются абсолютно новые методы выявления подозрительных операций. Основаны данные приемы на принципах математического анализа. Используя их, внимательный аналитик сможет распознать сфабрикованные документы.
В последние годы квалификация мошенников значительно возросла. В процессе совершения хищений активов и денежных средств часто преступники используют всевозможные высокотехнологические новинки. Не стоит на месте и квалификация тех, кто призван бороться с экономической преступностью.
В середине прошлого века ревизоры иногда использовали следующий прием – подсчитывали количество троек в документах и сравнивали с количеством восьмерок. Другой популярной парой цифр были единицы и четверки. Дело в том, что с минимальными затратами усилий тройки в первичных документах часто превращались в восьмерки, а единицы – в четверки. Если восьмерок было больше – ревизор мог предположить, что часть из них начинали свою жизнь тройками, и брался за лупу и арифмометр. Эффективность такого метода очень низкая, но альтернатив ему имелось не много. С появлением компьютеров стало очень легко анализировать большие объемы данных, но в основном, весь анализ сводился к простому суммированию. И только в последние годы анализ операций с целью выявления случаев мошенничества обогатился солидным научным инструментарием. Об одном из таких инструментов и пойдет речь ниже, но сначала обратимся к истории.
Числовые закономерности
В 1881 году астроном Саймон Ньюкомб, работая в библиотеке с книгой, содержащий таблицы логарифмов, обнаружил, что страницы в начале книги замусолены сильнее, чем остальные страницы. Надо отметить, что калькуляторов в те времена еще не придумали, и все расчеты производились на бумаге. Для сложных вычислений, таких как тригонометрические и логарифмические, использовались специальные книги, содержащие таблицы значений множества чисел. Некоторые из нас, в общем, еще помнят «Таблицы Брадиса», пользоваться ими учили в средней школе. Речь в дальнейшем идет как раз о подобной книге. Подобная странность наблюдалась не только на одном конкретном экземпляре, но и на большинстве других. Причина такой неравномерности была очевидна: студенты, пользующиеся таблицами логарифмов, чаще всего интересовались значением логарифма числа, начинающегося с единицы, затем с двойки, и так далее. Логарифмы чисел, начинающихся с девятки, интересовали студентов менее всего.
Размышляя на эту тему, Ньюкомб первым открыл эмпирический закон распределения чисел. Он гласит, что если мы случайным образом выберем любое число из таблицы, содержащей физические значения или статистические данные, вероятность того, что оно будет начинаться с единицы, приблизительно равна 0,301. Если бы все начальные цифры чисел встречались с одинаковой вероятностью, то такая вероятность должна была равняться 0,1. Ньюкомб опубликовал статью об этом наблюдении, но она была проигнорирована научным сообществом.
Формула Бенфорда
В 1938 году американский физик Фрэнк Бенфорд листал в библиотеке таблицы логарифмов. Обнаружив ту же закономерность, что и Ньюкомб, он пошел гораздо дальше. Бенфорд проанализировал справочные данные о площадях поверхности 335 рек, химических параметрах тысяч химических соединений, номерах домов из адресного справочника, результатах бейсбольных матчей. В итоге ученый обнаружил, что везде соблюдается одна и та же закономерность: чисел, начинающихся с единицы, гораздо больше, чем начинающихся с любой другой цифры. Пытаясь выразить обнаруженную закономерность математически, Фрэнк Бенфорд вывел формулу, описывающую вероятность (p) того, что случайная десятичная дробь будет начинаться с числа n:
p = lg(n+1)-lg(n)
Из формулы ясно: чем меньше цифра, тем больше вероятность того, что с нее будет начинаться случайная десятичная дробь (см. таблицу).
Таблица. Вероятность появления цифры первой в случайной десятичной дроби.
| Цифра | Частота появления первой, по Бенфорду |
| 1 | 0.30103 |
| 2 | 0.176091 |
| 3 | 0.124939 |
| 4 | 0.09691 |
| 5 | 0.0791812 |
| 6 | 0.0669468 |
| 7 | 0.0579919 |
| 8 | 0.0511525 |
| 9 | 0.0457575 |
Справедливость формулы подтверждали результаты многих практических исследований. Бенфорд назвал данную закономерность «законом аномальных чисел». Слово «аномальные» появилось в результате того, что одни данные соотносились с обнаруженным законом лучше, чем другие, но общая тенденция все равно прослеживалась. Площади рек и номера домов соответствовали закону идеально, а таблицы удельных теплоемкостей – несколько хуже. Бенфорд считал, что его закон применим только к тем числам, между которыми не имеется связующих закономерностей.
История и на этот раз распорядилась по-своему. Закон, открытый Бенфордом, стали называть «Законом Бенфорда», но практического применения он так и не получил, оставаясь в разряде математических курьезов.
Наблюдения и закономерности
В 1961 году Роберт Пинкхем заметил еще одну закономерность. Закон Бенфорда работает и при любой единице измерений! То есть если измерить площадь рек в квадратных километрах и исследовать частоту появления разных чисел в качестве первой цифры обнаружится, что эта частота соответствует Закону Бенфорда. Даже если измерить площадь тех же самых рек в квадратных футах – результат также будет соответствовать Закону Бенфорда. Подобные утверждения справедливы и для различных валют. Например, если цены, выраженные в долларах, соответствуют распределению Бенфорда, то это не изменится даже при их пересчете по курсу в евро или рубли.
В 1986 году физик Дон Лемонс первым обратил внимание на простое обстоятельство, которого наука прежде не замечала: луж больше, чем прудов, а прудов больше, чем океанов. Из этого следует, что водоемов площадью от 10 до 20 аров (гектаров, квадратных километров и пр.) больше, чем площадью от 20 до 30 аров. А площадью от 100 до 200 аров больше, чем площадью от 200 до 300 аров, и так далее.
Простым языком Закон Бенфорда можно описать так: маленьких вещей в мире всегда больше, чем больших. Маленьких озер всегда больше, чем больших, маленьких камней – больше, маленьких книг – больше, фотографий, на которых изображен один человек, – больше, чем групповых, низких домов – больше, чем многоэтажных, незначительных аварий на дорогах – больше, чем серьезных. В бухгалтерии – проводок на маленькие суммы – больше, чем на большие. Почему так происходит – закон не объясняет, поскольку он является эмпирическим, но происходит все именно так.
Бенфорд-последовательность или нет?
Долгое время Закон Бенфорда так и не имел никакого практического применения. Только в последнее время его начали использовать как серьезный аналитический инструмент. Все началось с того, что американский математик Марк Нигрини сообразил, что Закону Бенфорда должны подчиняться не только площади рек, но и числа в налоговых декларациях и данные бухгалтерского учета.
В 1997 году Нигрини и Миттермайер разработали шесть математических тестов, основанных на Законе Бенфорда. Эти тесты первыми были введены в практику международной аудиторской компанией «Эрнст и Янг» для анализа и выявления нерегулярностей в данных клиентов при аудите.
Первый вопрос, на который должен ответить аудитор при проведении теста – является ли набор неких данных Бенфорд-последовательностью или нет. То есть соответствует ли он распределению Бенфорда. Самый простой способ – представить, откуда эти данные берутся. Если они получаются в результате естественного течения событий или присутствуют в природе «сами по себе» – скорее всего они будут соответствовать Закону Бенфорда. Вот некоторые примеры данных, соответствующих Закону Бенфорда:
- номера платежных поручений от различных покупателей (вся совокупность);
- суммы платежей от покупателей;
- суммы в авансовых отчетах;
- остатки товаров на складах;
- номера домов в адресах клиентов.
Не соответствуют Закону Бенфорда:
- почтовые индексы;
- номера телефонов (первые цифры – номер АТС);
- выигрышные номера в лото и рулетку (здесь цифры – лишь символы, их легко можно заменить, например, на буквы);
- любые объемы данных, размер которых не достаточен для применения статистических методов;
- суммы платежей от покупателей и объемы заказов, если продается несколько позиций одной номенклатуры. Допустим, мы реализуем авторучки ценой 99 долларов за каждую. Чаще всего покупают всего одну ручку. Поэтому в большинстве случаев первой цифрой в сумме платежа будет девятка. На втором месте – единица (оплата за две ручки – 198 долларов). На третьем месте – двойка (оплата за три ручки – 297 долларов) и т. д.
Условия применения
Существуют определенные условия, которым должны соответствовать наборы данных, предполагаемые к анализу по закону Бенфорда. Во-первых, геометрическое распределение. Это означает, что источник данных для анализа должен быть геометрическим источником данных. Правда, на практике такое соответствие соблюдается редко. Но исходные данные должны «стремиться» к геометрическому распределению.
Во-вторых, данные должны относиться к одинаковым объектам. Нельзя смешивать данные платежных поручений и данные адресов клиентов.
В-третьих, не должно быть ограничений для чисел по максимуму и минимуму. Если есть некая граница, (допустим, предельный размер расчетов наличными), то такая совокупность данных уже может не являться идеальной Бенфорд-последовательностью.
В-четвертых, отсутствие системы нумерации. Числа не должны быть составными системами. Например, набор цифр в ИНН не будет являться Бенфорд-последовательностью, так как первые две цифры в ИНН – код региона, вторые две – код инспекции, а последняя цифра – контрольная – вычисляется из всех предыдущих.
Тесты могут проводиться как на соответствие Закону Бенфорда, так и на несоответствие. Допустим, мы знаем, что номера приходных кассовых ордеров и суммы, в них указанные, должны соответствовать Закону Бенфорда. Но при анализе выясняется, что они не соответствуют. Следовательно, высока вероятность того, что эти приходные ордера фальсифицированы бухгалтером. Очевидно, он их создавал и нумеровал самостоятельно, выдумывая цифры «из головы».
На практике применяются следующие тесты:
Анализ «первой цифры» и «второй цифры». В этом тесте набор данных анализируется на частоту появления различных цифр: от 1 до 9 в качестве первой цифры в числе и от 0 до 9 как второй цифры в числе. Результирующие данные отображаются в таблице или в форме графика. При наличии значительных расхождений с эталонными значениями проводится специальное исследование, которое должно дать ответ на вопрос о причине таких расхождений.
Анализ «первой и второй цифры». Этот тест исследует частоту появления цифр от 10 до 99 в начале чисел. Результат представляется в виде графика, содержащего сравнение экспериментальных данных с эталонными. Комбинации начальных цифр, не соответствующие эталонному значению, считаются «аномальными». Данный тест эффективен для выявления искусственных ограничений по достижении некоторого установленного лимита. Допустим, в организации существует особый порядок отчетности по затратам более 35000 рублей. При анализе выясняется, что количество расходов, начинающихся с 34 и 33, значительно превышает норму. При этом расходы, начинающиеся с 35 и 36, появляются крайне редко. Такая ситуация свидетельствует о возможном искусственном занижении сумм некоторых расходных операций.
Анализ «с первой по третью цифру». Тест определяет частоту появления комбинаций цифр с 100 до 999 в первых трех знаках набора данных. Аналогичен предыдущему анализу, за исключением того, что требует более значительного объема исходных данных. На малых объемах (менее 10000 значений) часто возможны ложные случайные выбросы. Однако данный метод позволяет более тонко проводить анализ и улавливать тенденции, которые остались бы незамеченными при предыдущих тестах.
Анализ «округления». Тест проводится для того, чтобы измерить частоту появления различных цифр в последних знаках. Он позволяет обнаружить случаи систематического округления в тех наборах данных, где округления быть не может по определению (например, пробег автомобилей, показания счетчиков расхода электроэнергии или количества сделанных копий у копировального аппарата). В простейшем случае частота появления цифры 0 в конце чисел должна быть равна 10 процентам, а 25, 100, и 1000 – 4, 1 и 0,1 процента соответственно.
Анализ «дубликатов». Он заключается в следующем. Сначала находятся числа с одинаковыми значениями. Затем подсчитывается частота проявления каждого из этих чисел. После чего выводится таблица результатов, отсортированных по убыванию количества совпадений. Анализ позволяет выявить случаи аномального присутствия в наборе данных одинаковых значений.
Области применения этих методов достаточно обширны. Они используются при внутренних расследованиях, налоговых проверках, внешнем аудите, контроллинге, оценке.
Программное обеспечение анализа
Конечно, анализ на соответствие закону можно проводить и при помощи программы Excel или рассчитывать закономерности на бумаге (помните историю открытия Закона?). Однако ведущие мировые производители программных комплексов, разработанных для аудита или выявления случаев мошенничества, давно встроили тесты на основе Закона Бенфорда в свои программы. С их помощью аудитор или ревизор за несколько секунд может обработать огромный массив исходной информации, выявить аномальные результаты и отобрать самые подозрительные транзакции для более детальной проверки. Аудитору можно порекомендовать пакеты: ACL компании ACL Services Ltd, IDEA от компании CaseWare International Inc. или ActiveData компании InformationActive Ltd. В России подобный функционал встраивается в некоторые версии программы AuditNET одноименной компании.
Автоматизация упростит проверку
Антон Бурцев, технический директор компании AuditNET
«Анализ данных с использованием закона аномальных чисел позволяет выявить такие негативные явления как мошенничество, часто встречающиеся неумышленные ошибки и операционную неэффективность (например, слишком большое количество операций с малыми суммами).
Закон Бенфорда помогает обнаружить систематические искажения таких операционных данных, как:
- суммы бухгалтерских проводок;
- суммы страховых выплат;
- стоимость гарантийного ремонта;
- суммы выставленных счетов;
- объемы поставок;
- суммы в налоговых декларациях.
Применять тесты на основе закона Бенфорда эффективнее на предприятиях с интенсивной операционной деятельностью, так как данная методика работает только при анализе больших массивов данных.
Закон Бенфорда позволяет не только отыскать аномалии в статичных данных, но и организовать постоянный мониторинг операционной деятельности организации. При этом оценивать данные можно как в денежных, так и в натуральных величинах. Закон Бенфорда формален, поэтому все проверки могут быть полностью автоматизированы. Это позволяет проверять достоверность абсолютно всех операционных данных без привлечения дополнительных человеческих ресурсов».
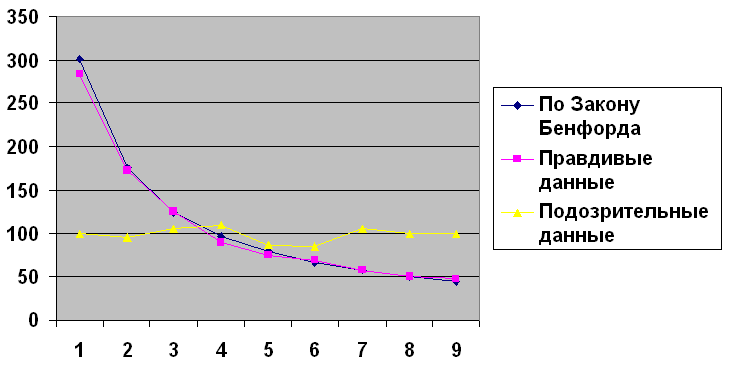
Схема. Примеры наборов данных, соответствующих и не соответствующих распределению Бенфорда
Подписи к осям:
Горизонталь – первая цифра в числе
Вертикаль – количество чисел (наблюдений)