Измеренная угроза

Угрозы для капитализации компании можно минимизировать с помощью инструментов измерения риска . Некоторые из них давно используются в мировой практике и применимы на российском рынке .

Говоря об измерении рисков капитализа-ции¹ , необходимо перейти от уровня котировок акций к уровню доходностей. Полный акционерный доход на акцию за один период определяют как:

где P₀ – цена акции в начале периода (например, $40);
P₁– цена акции в конце периода (например, $48);
D – выплаченные дивиденды (например, $2).

В данном случае полная акционерная прибыльность акции за один период равна 25%. Как правило, при анализе рисков нас интересует доходность акций за относительно короткий период, в течение которого не выплачиваются дивиденды по акциям. Поэтому для коротких интервалов доходность акций равна процентному изменению в их цене² .

Риск капитализации можно разложить на две компоненты: рыночный риск и специфичный риск. Рыночный риск измеряется так называемой бетой (), частью волатильности котировок, которая может быть связана с колебаниями всего рынка. Котировки большинства акций растут, когда весь рынок идет вверх, и снижаются, когда рынок падает.

Специфичный корпоративный риск относится к той части волатильности котировок акций, которая является уникальной (индивидуальной) для данной компании. Например, компания, которая выпускает финансовую отчетность с результатами ниже ожидаемых аналитиками, может значительно снизить свою капитализацию в день выхода отчетности независимо от величины компании или направления движения всего рынка в этот день.

Измерение полного риска : VaR

Рисковая стоимость – вероятностный показатель риска как для отдельных активов, так и для инвестиционных портфелей. Часто используется как приближенное значение «максимальных потерь, реально возможных при нормальном состоянии рынка». Особенно популярен как интегральный показатель риска среди банкиров, дерива-тивных дилеров и корпоративных риск-менеджеров. Несколько менее популярен среди управляющих инвестиционными портфелями.

Рисковая стоимость (Value at risk, VaR) – это показатель подверженности актива или портфеля активов риску снижения рыночной стоимости (капитализации). Для того чтобы ее вычислить, сначала необходимо получить вероятностное распределение доходностей (процентных изменений в стоимости) портфеля за определенный интервал времени – VaR-распределение. VaR облегчает прямое сравнение риска между различными портфелями и активами и дополняет, но не заменяет собой другие показатели риска.

Проиллюстрируем вычисление VaR на примере международного портфеля акций с помощью двух наиболее простых и популяр ных методов вычисления – исторического и ковариационного.

Историческая VaR

В качестве иллюстрации используется индекс «FTSE 100 Index» – индекс акций 100 наиболее крупных по капитализации компаний на Лондонской фондовой бирже (ЛФБ). Индекс включает в себя компании, которые составляют 80% капитализации ЛФБ и является на ней самым популярным индексом. Один из способов вычислить VaR – использовать временной ряд доходностей актива/ портфеля в прошлом и предположение о том, что в целом динамика изменений стоимости портфеля будет сохраняться и в будущем.

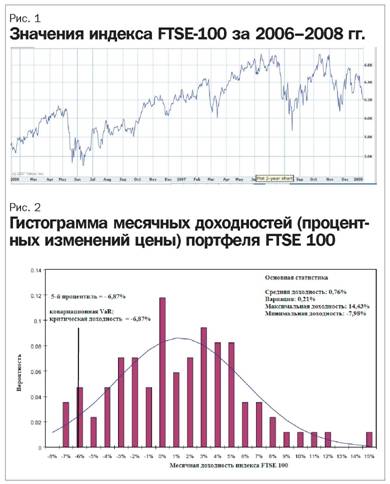
На горизонтальной оси рис. 2 показаны месячные доходности, а на вертикальной оси – процентное распределение месячных доходностей за период более 15 лет. Данная гистограмма может быть использована как эмпирическое вероятностное распределение. Например, крайний правый столбик на гистограмме означает, что в 1% случаев процентные изменения стоимости индекса за месяц были более чем 14%. Поэтому можно предположить, что имеется 1%-я вероятность, что в следующем месяце индекс вырастет тоже на 14% и более. В качестве примера возьмем международный инвестиционный портфель стоимостью 1 млн, полностью инвестированный на Лондонской бирже в акции, входящие в индекс FTSE-100 в таких же пропорциях, как на графике (индексный фонд). Для данного портфеля 95% VaR с месячным горизонтом означает процентные потери в стоимости, которые портфель может понести не чаще чем в пяти месяцах из ста. Используя исторические данные 95%-й VaR рассчитывается как:

где R 0,05 означает 5-й процентиль исторических месячных доходностей индекса FTSE-100. На графике 5-й процентиль показан вертикальной линией, и он равен -6,87%, что в денежном выражении составляет 68700

Таким образом, можно ожидать, что стоимость чистых активов (NAV) паевого фонда может снизиться более чем на 68 700 не чаще чем в пяти месяцах из последующих 100.

Ковариационная VaR

Самое главное условие применения ковариационного подхода – предположение о том, что доходности имеют нормальное распределение, которое полностью характеризуется математическим ожиданием и вариацией. Для вычисления риска актива достаточно знать вариацию данного актива. Это наиболее популярный и дешевый способ вычисле ния рисковой стоимости.

Рисковая стоимость для одного актива и одного периода

Для вычисления этого показателя используется тот факт, что 5% нормального распреде ления лежат ниже (слева) от 1,65 стандартного отклонения от среднего. Для индекса FTSE-100 средняя доходность за месяц равна 0,76% и месячная вариация – 0,21%. При рыночной стоимости портфеля NAV = млн, месячный 95%-VaR равен:

VaR облегчает прямое сравнение риска между различными портфелями и активами и дополняет, но не заменяет собой другие показатели риска.

В данном случае 5-й процентиль доходности портфеля, вычисленный ковариационным способом, практически равен 5-му процен-тилю эмпирического распределения доходности индекса. Для измерения стандартного отклонения было использовано историческое стандартное отклонение доходностей индекса за 85 месяцев.

Рисковая стоимость для нескольких активов и одного периода

В данном случае надо вычислить VaR того же самого портфеля FTSE-100, но для фонда, который расположен в долларовой зоне. Таким образом, полный портфель состоит из двух позиций: портфель акций, номинированных в фунтах стерлингов, и спот-позиция в обменном курсе для конвертирования фунтов в доллары США. На момент вычисления обменный курс был равен $1,629 за 1. Таким образом, стоимость портфеля акций в долларах США равна $1 629 000. Комбинированный портфель инвестора, ведущего расчеты в долларах США, включает позицию $1 629 000 в FTSE-100, а также позицию в обменном курсе. Одномесячный VaR портфеля акций равен:

( в этом случае со знаком «минус», так как это возможные потери, но часто минус опускается, так как все понятно и так). Так как VaR портфеля рассматривается в данном случае в изоляции, то данный показатель риска называется недиверсифицированным VaR позиции в акциях.

Затем вычисляется недиверсифицированный VaR позиции в обменном курсе:

где являются ожиданием и стандартным отклонением месячных процентных изменений в обменном курсе между британским фунтом стерлингов и долларом США. Среднее значение и стандартное отклонение обменного курса вычисляется по историческим данным:

Таким образом, недиверсифицированная рисковая стоимость позиции в обменном курсе равна

Для вычисления полной (совокупной) рисковой стоимости портфеля используется свойство двумерного нормального распределения:

где и является корреляцией между доходностью индекса FTSE-100 и месячными процентными изменениями в обменном курсе. Подставляя соответствующие значения, получаем:

Данная рисковая стоимость называется диверсифицированной рисковой стоимостью, или одномесячным VaR, который одновременно отражает и риск капитализации акций, и риск обменного курса, а также корреляцию между ними.

Управляющему портфелем следует ожидать, что портфель может потерять более 8% своей стоимости (NAV) не чаще, чем в пяти месяцах из 100. Диверсифицированный VaR снижается за счет негативной корреляции между доходностью акций и колебаниями обменного курса. Он значительно меньше, чем просто сумма двух недиверсифицированных VaR.

Рисковая стоимость для нескольких периодов

Чтобы посчитать VaR для более длительного периода, используется предположение о том, что доходности являются независимыми и стабильными во времени (стационарными). Если это условие выполняется, то VaR за несколько периодов равен произведению VaR за один период на квадратный корень из количества периодов. Например, диверсифицированный 95%-й VaR портфеля FTSE-100 на один квартал равен 95%-му VaR на один месяц, умноженному на квадратный корень из трех: $49 470 x 1,7321 = $85 685. Если требуется 10-дневный VaR, аналитики обычно вычисляют однодневный 99% VaR и используют формулу:

Дополнительный пример вычисления VaR

Допустим, у управляющего портфелем международных акций имеется позиция в акциях компании Microsoft стоимостью $10 млн. Волатильность акций Microsoft составляет 2% в день (около 32% в год). Требуется посчитать 99%-й VaR с горизонтом в 10 дней. Стандартное отклонение доходностей портфеля за один день равно $200 000. Стандартное отклонение доходностей за 10 дней равно:

Считается, что ожидаемое значение доходности портфеля за короткий период времени равно нулю. Также мы предполагаем, что изменения в цене портфеля имеют нормальное распределение. Так как N (–2,33) = 0,01, то VaR равен:

2,33 x $632 456 = $1 473 621.

Также у управляющего портфелем имеется длинная позиция в акциях AT & T стоимостью $5 млн. Дневная волатильность AT & T равна 1% (около 16% в год). Стандартное отклонение за 10 дней равно:

VaR = $158 144 Ч 2,33 = $348 405.

Теперь рассмотрим VaR для портфеля акций, состоящего из Microsoft и AT & T .

Корреляция между изменениями цены акций равна 0,3. Согласно статистической формуле стандартное отклонение портфеля из двух акций равно:

В данном случае и

Стандартное отклонение изменений в цене портфеля за один день равно 220 227. Таким образом, 10-дневный 99%-й VaR для портфеля равен:

В итоге выигрыш от диверсификации равен: ($1 473 621 + $368 405) – $1 622 657=$219 369.

Измерение системных рисков : бета , capm и многофакторные модели

Коэффициент бета () в финансах и инвестициях является показателем волатильности акций по отношению к остальному рынку. индивидуальных компаний вычисляется при помощи регрессионного анализа. Она является ключевым параметром в модели CAPM³, измеряющей ту часть статистической вариации акций, которая не может быть ликвидирована посредством диверсификации портфеля, так как коррелирует с колебаниями в стоимости других акций в портфеле. Коррелированный риск, измеряемый , создает практически весь риск в диверсифицированных портфелях. для актива внутри портфеля равна:

где r_a – процентные изменения (доходность) в рыночной стоимости самого актива; r p – процентные изменения в рыночной стоимости портфеля, в который входит данный актив;

Cov ( r_a , r_p) – ковариация между доходностью актива и доходностью портфеля. Использованный в модели CAPM портфель является рыночным, то есть содержащим все рискованные активы на рынке, поэтому r p в формуле заменяется на r m – доходность рынка (процентные изменения в величине индекса всего рынка).

Также часто называется финансовой эластичностью актива или коррелированной волатильностью и считается показателем чувствительности доходности актива к колебаниям рынка. измеряет недиверси-фицируемый или системный риск. Изменения в необходимо отличать от изменений в доходности акций. Например, какой-либо сектор экономики может быть в отличном положении и иметь хорошие перспективы, но не коррелировать с индексом всего рынка. В результате для компаний этого сектора будет низкой. Но это не будет означать, что инвестиции в данный сектор не являются привлекательными. Бета является показателем риска, а не привлекательности компании или сектора для ин вестиций.

Для вычисления беты используется линейная регрессия доходности акций компании на доходность портфеля (биржевого индекса). Регрессионная линия в данном случае называется Security Characteristic Line ( SCL ) и имеет следующую формулу:

где _a – коэффициент альфа акций, a – бета акций, а r m , t – рыночная премия за риск (разница между доходностью рынка и безрисковой ставкой). Например, в определенный год фондовый индекс вырос на 25% по сравнению с безрисковой ставкой, а управляющий инвестиционным фондом получил 50% доходности своего портфеля. Если бета портфеля равна 3,0, то это говорит о том, что дополнительная по сравнению с рынком доходность портфеля недостаточна для того, чтобы компенсировать инвесторам избыточный риск по сравнению с рыночным портфелем (так как бета всего рынка по определению равна 1,0). Если же портфеля равна 1,5, это означает, что управляющий портфеля получил более высокую доходность по сравнению с рынком, чем предполагается риском портфеля. По определению всего рынка равна 1,0, а акции индивидуальных компаний ранжируются по отношению к рынка. Акции, котировки которых колеблются больше, чем рынок в целом, имеют больше 1,0, и наоборот. Например, если акций равна 2,0, это означает, что при росте рынка на 3% котировки акций вырастут на 6%. Отрицательная означает, что котировки акций движутся в противоположном с рынком направлении. Считается, что «агрессивные» акции имеют больше 1,0. Такие акции дают хороший доход на растущих рынках, так как котировки растут быстрее рынка. Акции с меньше 1,0 считаются «защитными» акциями, так как при снижении рынка они снижаются меньше, чем рынок в целом. Чем больше , тем больше волатильность акций и тем более рискованной считается данная акция. Поэтому ожидается, что чем выше , тем больше должна быть ожидаемая доходность акции, для того чтобы компенсировать повышенный риск. Например, если рынок в целом имеет доходность 8% в год, то акция с бетой 1,5 должна иметь ожидаемую доходность 12% в год. Согласно модели CAPM ожидаемая доходность акций определяется по формуле:

где: K E – стоимость акционерного капитала для компании (ожидаемая инвесторами доходность акций); R F – безрисковая ставка; R M – доходность всего рынка;

где D – стоимость долгового капитала фирмы; Е – акционерная стоимость фирмы (стоимость акционерного капитала); V – стоимость бизнеса компании, V = D + E . Если компания не имеет долговых обязательств, то a = E , то есть актива (всей фирмы) равна акционерного капитала. Теоретически не имеет нижних или верхних границ. Она может быть равна 0 ( наличных денежных средств). Однако сам факт того, что = 0, не означает, что данный актив не имеет риска, а говорит, что стоимость актива абсолютно не коррелирует с рынком. Для компаний, чьи акции котируются на глобальных (международных) биржах, и для стран, чьи фондовые рынки интегрированы в международный рынок, употребляется так называемая международная версия модели CAPM :

где R_f – международная безрисковая ставка ( ставка по евродолларам);
i,w – чувствительность котировок акции «i» к колебаниям глобального рынка (глобального индекса);

где чувствительность котировок акций компании «i» к колебаниям домашнего рынка;

чувствительность домашнего рынка к колебаниям глобального рынка. В настоящее время используются, как правило, многофакторные модели, согласно которым ожидаемая доходность акций моделируется как линейная функция различных макроэкономических факторов и рыночных индексов. Чувствительность изменений котировок по отношению к каждому фактору риска определяется бета-коэффициентом данного фактора риска:

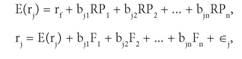
где E ( r_j ) – ожидаемая доходность акций;
RP _k – премия за риск определенного риск-фактора;
r _f – безрисковая ставка;
F _k – определенный макроэкономический или отраслевой фактор;
b _jk – чувствительность стоимости акций к изменению риск-фактора k (также называется факторной нaгрузкой);
_j – диверсифицируемый специфичный риск отдельного актива.

Обычно в качестве основных объясняющих факторов риска в данной модели используются следующие факторы:

• изменения в темпах инфляции;
• изменения в ВВП;
• изменения в спрэде на корпоративные облигации по сравнению с государственными облигациями;
• изменения в кривой доходности облигаций;
• изменения в ставке краткосрочных кредитов;
• разница между ставками долгосрочных и краткосрочных кредитов;
• изменения в цене нефти, золота и других сырьевых товаров;
• изменения в обменных курсах основных валют.

Измерение портфельного риска : tracking error

Банк международных расчетов ( BIS ) выделяет из риска капитализации системный (общий) риск. Он относится к изменениям капитализации, возникшим в связи с колебаниями на финансовых рынках (изменения в процентных ставках, обменных курсах, ценах на сырье и т.д.). На широко диверсифицированный портфель в первую очередь влияют

колебания совокупной стоимости фонда, а также разница между доходностью реального фонда и его эталона. Именно в этом смысле понятие «риск капитализации» применимо к диверсифицированным портфелям. В зависимости от подхода к управлению инвестиционным портфелем существуют два вида рисков капитализации – активный риск и риск слежения. Активный риск связан с подбором акций и других ценных бумаг для портфеля и динамикой их котировок относительно эталонного портфеля. В этом случае опасность заключается в приобретении акций с доходностью ниже средней по эталонному портфелю.

На широко диверсифицированный портфель в первую очередь влияют колебания совокупной стоимости фонда, а также разница между доходностью реального фонда и его эталона.

Риск слежения – это риск неверного выбора эталонного портфеля (доходность управляемого портфеля растет, когда доходность эталона снижается). В таком случае считается, что портфель имеет значительную погрешность слежения ( tracking error ) и управляющий портфелем не инвестирует в те категории акций, для которых предназначен данный портфель. Ошибка слежения – показатель того, насколько близко портфель следует за своим эталоном (как правило, индексом рынка). Есть несколько подходов к определению погрешности слежения. Под ней может пониматься простая разница между процентными измерениями в стоимости портфеля и его эталона (индекса рынка). Однако чаще ошибка измеряется стандартным отклонением разницы между процентными изменениями стоимости портфеля и индекса:

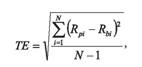
где R _pi – процентные изменения актива в период «i»;

R _bi – процентные изменения (доходность) эталона (индекса рынка) за период «i»; N – количество периодов.

Многие портфели акций управляются по подобию эталона и зачастую должны полностью воспроизводить его прибыльность. В некоторых случаях портфели должны несколько отличаться от индекса для того, чтобы генерировать дополнительную прибыль сверх значения индекса или же экономить на управлении портфелем. Если погрешность отслеживания измеряется по реальным историческим данным, то она называется реализованной погрешностью слежения. Если же для ее вычисления используется математическая модель, то это прогнозируемая ошибка слежения.

Первая предназначена для анализа и отчетности, вторую применяют в основном риск менеджеры для контроля рисков портфеля. Для активно управляемых портфелей прогнозируемая ошибка слежения, как правило, ниже, чем реализованная ошибка слежения, иногда до двух раз.

Ошибка слежения является показателем навыков портфельного менеджера, а также показателем того, насколько активно управляется портфель

Низкая погрешность слежения означает, что портфель точно следует своему эталону и наоборот. Таким образом, погрешность слежения помогает инвесторам определить, как точно портфель имитирует свой эталон. Часто высокая погрешность слежения означает, что менеджер фонда принимает более рискованные инвестиционные решения, чем необходимо по задаче портфеля.

В конечном итоге ошибка слежения является показателем навыков портфельного менеджера, а также показателем того, насколько активно управляется портфель. Она может служить как целью для менеджера, так и ограничением, накладываемым на него.

Стратегия погрешности В зависимости от задач портфеля может быть две интерпретации стратегии слежения за индексом ( index tracking ):

1. Пассивная стратегия создания портфеля, точно воспроизводящего эталон.
2. Активная стратегия, которая стремится превзойти индекс или эталонный портфель, в то же время оставаясь в определенных рамках с точки зрения риска.

В некоторых случаях погрешность слежения определяется как остаточная волатильность следящего портфеля по отношению к вола-тильности эталонного портфеля. То есть погрешность слежения может быть рассчитана как стандартное отклонение остатков в линейной регрессии доходности имитирующего портфеля на доходность эталонного портфеля:

где – волатильность имитирующего портфеля слежения; – коэффициент корреляции между доходностью этого портфеля и эталонным портфелем.

Например, если волатильность портфеля составляет 20%, а коэффициент корреляции равен 0,95, это означает, что погрешность слежения равна 6,24%. Этот показатель имеет прямое применение в вычислении риска портфеля. Он используется для вычисления доходности портфеля с поправкой на риск ( appraisal ratio ) или же для определения требуемой доходности для данного уровня риска.

Погрешность слежения показывает, насколько хорошо портфель следует индексу или эталону, но ничего не говорит о доходности портфеля относительно эталона (так как портфель может как превосходить эталон по доходности, так и быть ниже его). В этом определенный недостаток погрешности слежения как меры риска. Но погрешность слежения используется для вычисления доходности портфеля с поправкой на риск или информационный коэффициент ( IR ), который равен:

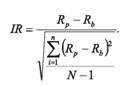
В числителе данной формулы разница в доходности активного или имитирующего портфеля, а в знаменателе – погрешность слежения. Чем выше IR , тем лучше доходность портфеля с поправкой на риск. Следует отметить, что при сравнении двух портфелей следует использовать один и тот же эталонный портфель.

Северный опыт

В качестве примера приведем погрешность слежения для Нефтяного фонда Норвегии. Министерство финансов Норвегии поручило норвежскому банку Norges Bank управлять Нефтяным фондом Норвегии. Министерство разработало эталонный портфель для Нефтяного фонда, а также определило максимальные размеры ошибки слежения. Основное ограничение состоит в том, какое количество рыночного риска может допускать управляющий национальным фондом банк. Это ограничение по риску носит характер максимального размера ошибки слежения.

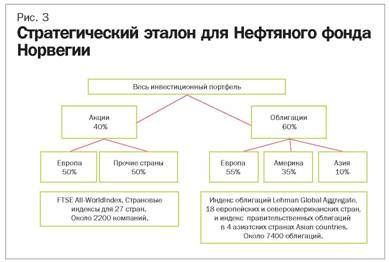
Эталонный портфель в данном случае – это гипотетический портфель, состоящий из набора акций и облигаций из различных стран, в которые фонд получил разрешение вкладывать средства. Состав эталонного портфеля отражает стратегический выбор Министерства финансов. Министерство финансов накладывает на банк, управляющий фондом, два ограничения. Первое – ограничение по аллокации активов по странам, биржам и видам активов (акций или облигаций). Например банк не может инвестировать более 50 и менее 30% капитала в акции.

Стратегический эталонный портфель состоит из конкретных акций и облигаций, его состав показан на рис. 3. Также Министерство финансов наложило ограничения в виде максимально допустимой погрешности слежения: насколько доходность фонда может отличаться от доходности эталонного портфеля. Данная погрешность слежения не должна превышать 1,5% (150 базисных пунктов, равных одной сотой процента, 100 б.п = 1%). Для акций и облигаций вычисляется ожидаемая ошибка слежения (рис. 4).

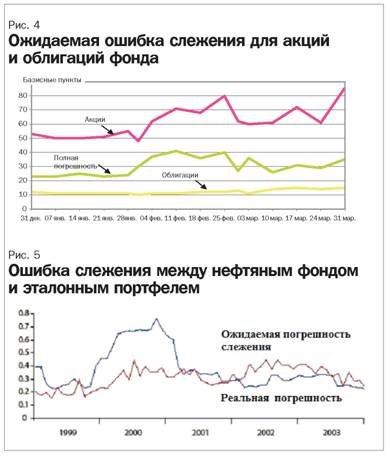
Стоимость эталонного портфеля зависит от колебаний рынка. Новые денежные поступления в фонд используются для того, чтобы приводить Нефтяной фонд Норвегии в соответствие со стратегическим эталонным портфелем. Полная ребалансировка должна производиться, только если отклонения от стратегического эталона становятся значительными и постоянными. Банк, управляющий нефтяным фондом, использует погрешность слежения как инструмент повседневного управления инвестиционным портфелем. На рис. 5 показаны два альтернативных показателя риска: прогнозируемая и реализованная погрешность слежения. Прогнозируемая погрешность вычисляется по историческим данным рыночной волатильности на протяжении последних нескольких лет. Этот показатель характеризуется относительно небольшой вариацией (ниже 1,5%). Реализованная погрешность слежения вычисляется на основе полученной разницы в доходностях за последние 12 месяцев. Эти две меры риска показывают разный уровень риска в 2000 году, когда рынки значительно колебались, но приблизительно одинаковый уровень риска в 2001–2003 годах.

¹О видах рисков, которым подвержена капитализация компании, см. № 3-4 2008.

² Также в аналитической литературе широко используется так называемая «логарифмическая доходность», которая равна  – 

³CAPM – Capital Asset Pricing Model , модель ценообразования на капитальные активы.