Оценка прогнозного искажения информации в генеральной совокупности модифицированным монетарным методом

Проанализированы недостатки известного монетарного метода при использовании выборочных статистических процедур в аудите. Показано, что при равных абсолютных значениях искажений в финан­совой информации применение монетарного метода может в различных условиях приводить к различным результатам. Предложена модификация монетарного метода, устраняющая указанные недостатки.

Международный стандарт аудита (МСА) 500 «Аудиторские доказательства» устанавливает, что при выборе объектов для проверки из оборота счета или из сальдо счета бухгалтерского учета аудитор может исполь­зовать такие методы, как: выбор всех объектов (сплошная проверка), выбор конкретных (специфических) объектов, формирование ста­тистической аудиторской выборки.

Согласно МСА 530 «Аудиторская выборка», при формировании статистической аудитор­ской выборки аудитор должен использовать приемы математической статистики для отбора ее элементов и оценки результатов проверки элементов, попавших в выборку. Подобная оценка, как поясняет МСА 530, заключается в экстраполяции искажения, выявленного в выборке, на всю генеральную совокупность (оборот или сальдо счета бухгалтерского учета), в результате чего аудитор определяет так называемое «прогнозное» искажение — наиболее вероятное искажение, содержащее­ся в генеральной совокупности.

В классических трудах по аудиту [1-4] рас­смотрен так называемый «монетарный» метод формирования статистической аудиторской выборки и оценки результатов проверки ее элементов. Особенность монетарного метода заключается в том, что элементом генеральной совокупности в нем является не натуральный объект (документ, операция), а денежная еди­ница — рубль. Выборка при использовании этого метода состоит не из «n» натуральных объектов, а из «n» рублей (элементом выбор­ки является рубль, входящий в стоимость по­павшего в выборку документа^[1]). Для оценки результатов проверки элементов подобной выборки авторы [1-4] предлагают способ, ос­нованный на гипотезе биномиального рас­пределения случайной величины (количества искажений в выборке).

Из теории вероятности известно: если в ге­неральной совокупности объемом N содержится М отмеченных (в нашем случае — ис­каженных) элементов, то количество m от­меченных (искаженных) элементов в выборке объемом п является случайной величиной, распределенной по биномиальному закону. Известно также, что при определенных усло­виях (N > 10n, М/N < 0,1) вероятность R би­номиального распределения может быть до­статочно точно определена по формуле Пуас­сона:

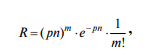
где N — объем генеральной совокупности; М — количество отмеченных (в нашем случае — искаженных) элементов в генераль­ной совокупности; n — объем выборки; m— количество отмеченных (искаженных) эле­ментов в выборке объемом n; р = M/N — относительное число отмеченных (искаженных) элементов в генеральной совокупности.

Задавшись приемлемым значением вероят­ности R (R = 0,1 или R = 0,05), с помощью фор­мулы Пуассона можно для конкретной вели­чины m (m = 0,1,2, ...) определить значения М и р — предельно возможное для заданной вероятности количество искаженных элемен­тов в генеральной совокупности (в абсолют­ных и относительных единицах).

Сумма же искажений в генеральной сово­купности (обозначим ее Р) по мнению авторов [1-4] может быть определена из относительной суммы искажений в выборке (обозначим ее х) с помощью зависимости:

где х = k/j; k — сумма искажения (руб.); j — учетная стоимость документа, содержащего искажение (руб.).

Например, генеральная совокупность со­стоит из 10 000 тыс. рублей (объем генеральной совокупности, выраженный в рублях, обо­значим через J, тогда J = 10 000 000 рублей). Объем выборки п = 100 рублей (100 «логиче­ских элементов»). В результате проверки вы­борочной совокупности установлено, что она содержит одно искажение (m = 1). Учетная стоимость документа, в котором обнаружено искажение, j = 5000 рублей, сумма искажения к = 500 рублей. Относительная сумма искаже­ния х =k/j = 500 / 5000 = 0,1. Иными словами, являющийся единицей выборки рубль, вхо­дящий в стоимость документа, содержащего искажение, «искажен» в размере 10 копеек (одной десятой). Из табличных значений би­номиального распределения, приведенных в [2-4], следует, что при m = 1 и n = 100 от­носительное число искаженных элементов в генеральной совокупности с 95-процентной вероятностью не превысит 4,7% (р = 0,047) (см. таблицу).

Тогда сумма искажений в генеральной со­вокупности с 95-процентной вероятностью не превысит величину:

Р = М • х = р • J • х = = 0,047 • 10 000 000 • 0,1 = 47 000 руб.

Отметим, что применение подобной мето­дики при количестве искаженных элементов в выборке более одного (m = 2, 3, 4, ...) не пред­ставляется обоснованным. Рассмотрим пример с исходными условиями, аналогичными пре­дыдущему (объем генеральной совокупности J = 10 000 000 рублей, объем выборки п = 100 рублей). Пусть выборочная совокупность содержит два искажения (m = 2). Пусть от­носительная сумма искажения в одном до­кументе х₁ = 0,1, в другом х₂ = 0,05. Тогда ве­личина Р, которую сумма искажений в гене­ральной совокупности не превысит с вероят­ностью 95%, по мнению авторов [3], может быть определена следующим образом:

где р₁ = 0,047 (при n = 100, m = 1); р₂ = 0,062 (при n = 100, m = 2) — см. таблицу.

Тогда:

= 0,047 • 10 000 000 • 0,1 + (0,062 - 0,047) х х 10 000 000 • 0,05 = 54 500 руб.

Очевидно, что подобная методика непри­емлема хотя бы в силу того обстоятельства, что при перемене местами документов, со­держащих искажения (х₁ = 0,05, х₂ = 0,1) , будет получен иной результат:

Р=р₁ • J • х₁ + (р₂ - р₁) • J • х₂ = 0,047 • 10 000 000 • 0,05 + (0,062 - 0,047) х 10 000 000 • 0,1 = 38 500 руб.

Таблица

Зависимость предельных значений искажений в генеральной совокупности от объема выборки и количества ошибок в выборке при 95-процентной вероятности

Объем выборки, n	Количество искажений в выборке, m
	0	1	2	3	4	5	6	7	8	9	10
25	11,3	17,6	*	*	*	*	*	*	*	*	*
30	9,5	14,9	19,5	*	*	*	*	*	*	*	*
35	8,2	12,9	16,9	*	*	*	*	*	*	*	*
40	7,2	11,3	14,9	18,3	*	*	*	*	*	*	*
45	6,4	10,1	13,3	16,3	19,2	*	*	*	*	*	*
50	5,8	9,1	12,1	14,8	17,4	19,9	*	*	*	*	*
55	5,3	8,3	11,0	13,5	15,9	18,1	*	*	*	*	*
60	4,9	7,7	10,1	12,4	14,6	16,7	18,8	*	*	*	*
65	4,5	7,1	9,4	11,5	13,5	15,5	17,4	19,3	*	*	*
70	4,2	6,6	8,7	10,7	12,6	14,4	16,2	18,0	19,7	*	*
75	3,9	6,2	8,2	10,0	11,8	13,5	15,2	16,9	18,4	20,0	*
80	3,7	5,8	7,7	9,4	11,1	12,7	14,3	15,8	17,3	18,8	*
90	3,3	5,2	6,8	8,4	9,9	11,3	12,7	14,1	15,5	16,8	18,1
100	3,0	4,7	6,2	7,6	8,9	10,2	11,5	12,7	14,0	15,2	16,4
125	2,4	3,7	4,9	6,1	7,2	8,2	9,3	10,3	11,3	12,2	13,2
150	2,0	3,1	4,1	5,1	6,0	6,9	7,7	8,6	9,4	10,2	11,0
200	1,5	2,3	3,1	3,8	4,5	5,2	5,8	6,5	7,1	7,7	8,3

Источник: составлено автором по материалам [3]

Кроме того, величина P, определенная по­добным образом, представляет собой некое «предельное» значение, которое возможная сумма искажений в генеральной совокупности не превысит с 95-процентной вероятностью.

Вместе с тем, как было указано выше, МСА 530 «Аудиторская выборка» содержит иное ука­зание: стандарт предписывает аудитору оценить не «предельное», а наиболее вероятное (про­гнозное) искажение, содержащееся в генераль­ной совокупности. Исходя из норм МСА 530, осуществив точечную оценку прогнозного ис­кажения в генеральной совокупности, аудитор далее должен оценить риск выборки, который может дать ответ на вопрос — какова вероят­ность того, что прогнозное искажение может превысить допустимое искажение (применяемый для анализируемой генеральной совокупности порог существенности — п. A3 МСА 530).

Оценка прогнозного (наиболее вероятного) искажения в генеральной совокупности на ос­новании применения «монетарного» метода рассмотрена в [5]. Предложенный в [5] способ оценки прогнозного искажения базируется на гипотезе нормального распределения раз­мера относительных искажений в генеральной совокупности.

Из математической статистики (теорема об оценке генеральной средней) известно, что генеральная средняя при нормальном рас­пределении может быть оценена по выбороч­ной средней. Тогда, подсчитав выборочную среднюю

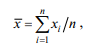
где хi — относительное искажение в 1-м эле­менте, попавшем в выборку; n — объем вы­борки, можно определить прогнозное (наи­более вероятное) искажение в генеральной совокупности:

где  = х — относительная сумма искажений в выборке.

Для рассмотренного выше примера (объем генеральной совокупности J = 10 000 000 рублей, объем выборки п = 100 рублей, относительная сумма искажений в выборке х = 0,1) наиболее вероятное искажение в генеральной совокуп­ности составит:

К = J/n • х = (10 000 000/100) • 0,1 = 10 000 руб.

Недостатком данного способа является то обстоятельство, что гипотеза о нормальном распределении размера относительных ис­кажений в генеральной совокупности не имеет статистического обоснования. В литературе по аудиту признанной является гипотеза о нормальном распределении случайной ве­личины — абсолютного размера искажений в генеральной совокупности; в свое время автором настоящей работы было получено экспериментальное подтверждение данной гипотезы. Размер же относительных искаже­ний представляет собой случайную величину, являющуюся частным от деления двух слу­чайных величин: абсолютного размера иска­жения и учетной суммы документа, содержа­щего искажение, причем закон распределения случайной величины (учетной суммы доку­мента) может быть различным. В силу этого гипотеза о нормальном распределении раз­мера относительных искажений в генеральной совокупности вряд ли может быть признана приемлемой.

В подтверждение того, что рассмотренные выше способы могут давать недопустимый разброс результатов, приведем простейший пример. Пусть, как и ранее, генеральная совокуп­ность состоит из 10 000 тыс. рублей (J = 10 000 000 рублей), объем выборки п = 100 рублей. Учетная стоимость документов варьируется в пределах от j= 5000 рублей до j = 50 000 рублей. Сумма обнаруженного ис­кажения, как и ранее, к = 500 рублей.

Если учетная стоимость документа, в ко­тором обнаружено искажение, j = 5000 рублей, то относительная сумма искажения x= k/j = 500/5000 = 0,1. В этом случае, как было ука­зано ранее, предельное значение, которое воз­можная сумма искажений в генеральной сово­купности не превысит с 95-процентной вероят­ностью, составит Р = 47 000 рублей, а наиболее вероятная сумма искажений в генеральной совокупности составит К = 10 000 рублей.

Если же учетная стоимость документа, в ко­тором обнаружено искажение, составит j = 50 000 рублей, то при том же абсолютном размере искажения относительная сумма ис­кажения х = k/j = 500/50 000 = 0,01. В этом случае предельное значение, которое возмож­ная сумма искажений в генеральной совокуп­ности не превысит с 95-процентной вероят­ностью, составит уже Р = 4700 рублей, а наи­более вероятная сумма искажений в генераль­ной совокупности будет равна К = 1000 рублей. Очевидно, что подобный разброс возможных результатов для аудитора неприемлем.

Указанных недостатков, присущих рассмот­ренным выше способам, можно избежать, если при применении монетарного метода относи­тельный размер искажений получать отноше­нием абсолютного размера выявленного ис­кажения не к учетной стоимости документа, содержащего искажение, а к его средней сто­имости, которая определяется из суммы учет­ных стоимостей всех документов, составляю­щих генеральную совокупность, и их количе­ства. В этом случае случайная величина (от­носительный размер искажений в генеральной совокупности) будет распределена по нор­мальному закону, поскольку будет связана со случайной величиной (абсолютным раз­мером искажений в генеральной совокупно­сти) постоянным множителем.

Рассмотрим возможность применения пред­ложенного способа на конкретном примере.

Пусть, как и в рассмотренных выше при­мерах, генеральная совокупность состоит из 10 000 тыс. рублей (J = 10 000 000 рублей), объем выборки п = 100 рублей. Учетная сто­имость документов варьируется в пределах от j = 5000 рублей до j = 50 000 рублей, а общее количество документов N = 1000. Сумма обнаруженного искажения, как и ранее, к = 500 рублей.

Средняя стоимость документа:

j = J/N = 10 000 000/1000 = 10 000 руб.

Относительный размер искажения:

х = к/j = 500/10 000 = 0,05.

Наиболее вероятное искажение в генераль­ной совокупности:

К= J/n • х = (10 000 000/100) • 0,05 = 5000 руб.

Сравним полученный результат с резуль­татом, который может быть определен с по­мощью известного метода, именуемого в ли­тературе методом «оценки средней суммы в расчете на единицу». Прогнозное искажение в генеральной совокупности с помощью этого метода может быть определено следующим образом:

К = N/n • к = (1000/ 100) • 500 = 5000 руб., 

где N = 1000 — объем генеральной совокуп­ности в натуральных единицах; п = 100 — объем выборки в натуральных единицах; к = 500 рублей — сумма искажений в выборке.

Как видим, результат идентичен получен­ному выше монетарным методом, что следует из очевидного равенства:

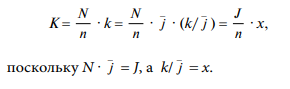
Таким образом, при использовании моне­тарного метода в ходе осуществления выбо­рочных статистических процедур следует абсолютную сумму искажений в выборке от­носить не к учетной стоимости документа, а к его средней стоимости.

Литература

1. Адамс Р. Основы аудита. — М. : Аудит-Юнити, 1995. — 560 с.

2. Аренс А., Лоббек Дж. Аудит. — М. : Финансы и статистика, 1995. — 560 с.

3. Аудит Монтгомери / Ф. Дефлиз, Г. Дженик. В. О'Рейли и др. — М. : Аудит, 1997. — 541 с.

4. Робертсон Д. Аудит. — М. : Контакт, 1993. — 496 с.

5. Логиненков А.В. Классификация и систематизация статистических выборочных методов в ау­дите // Аудит и финансовый анализ. — 2014. — № 1. — С. 173-205.

 

---

^[1] В указанной выше литературе подобный документ, стои­мость которого содержит наш денежный элемент совокуп­ности - рубль, называется «логическим элементом»