Улучшенный расчет разводненной прибыли на акцию

По материалам: IFRS

Одна из самых, на наш субъективный взгляд, интересных работ из всех представленных на прошедшем недавно Восьмом исследовательском форуме IASB была посвящена улучшению действующего подхода к расчету разводненной прибыли на акцию по стандарту МСФО (IAS) 33 “Прибыль на акцию”. Сами работы и записи обсуждений по ним не сразу были выложены на сайте разработчиков МСФО, но теперь с ними, наконец, можно ознакомиться в полном объеме. Предлагаем чуть детальнее рассмотреть, что именно предложили исследователи из Австралии - Варрик Ван Зил (Warrick Van Zyl) и Энрико Улиана (Enrico Uliana). По ссылке можно ознакомиться с презентацией в оригинале, а ее аудиозапись доступна здесь.

В своем исследование авторы сравнивают между собой три различных метода расчета разводненной прибыли на акцию. Первый оговорен в IAS 33, второй представляет собой его улучшенную версию “Earnings adjusted method” (“Метод скорректированной прибыли”), и это именно то, что предлагают авторы сегодняшнего исследования. Еще один подход идет как альтернатива – “Treasury option method” (“Метод казначейских опционов”) разбирался в работе 2002 года Core, Guay & Kothari, и он также представляется усовершенствованной версией классического подхода IAS 33, хоть и не без недостатков.

По мнению авторов, самым слабым из трех перечисленных является именно метод в IAS 33. Что же с ним не так? А хотя бы то, что он очень старый. Логика расчета опирается на древнейшее положение о бухгалтерских принципах американского APB (Opinion No. 15), страшно подумать, 1969 года! С тех пор, конечно, многое изменилось - особенно в 70-е годы, с появлением международных стандартов бухгалтерского учета (IASs).

Еще больше изменений принес период 2002-2005 гг., когда стали появляться уже международные стандарты финансовой отчетности, в частности, IFRS 2 “Выплаты на основе акций”, после чего немного изменился расчет цены исполнения в IAS 33 - добавилось вариативности, но кроме этого, все осталось преимущественно как в далеком 1969-м.

Величина размытой прибыли на акцию является в современном бухгалтерском мире одним из наиболее часто используемых показателей, и на него очень часто ориентируются инвесторы. Авторы в своем исследовании изучают вопрос на примере опционов на акции работникам, но отмечают, что логика их рассуждений легко применима к другим инструментам (например, конвертируемым облигациям), просто опционы на акции очень иллюстративны.

“Классический” подход IAS 33

Что предлагает по этому поводу стандарт IAS 33? Он исходит из того, что держатели опционов исполняют их немедленно, и что для исполнения их компания выпускает новые акции. В то же самое время компания использует поступления от выпущенных опционов на акции в целях обратного выкупа уже обращающихся акций. Чистым результатом этих двух противоположных транзакций станет увеличение общего числа акций - его нужно будет ставить в знаменатель формулы для расчета, чтобы определить величину размытой прибыли:

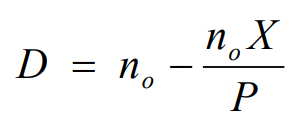
где Р - текущая цена акций, n0 - число опционов, Х - цена исполнения. То же самое можно записать по-другому:

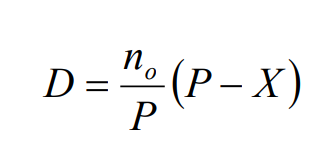
Выражение в скобках, (P-X) – это, конечно, внутренняя стоимость опциона. Это единственное, на что сегодня обращает внимание стандарт, полностью игнорируя факт нахождения опциона “в деньгах”, и игнорируя временную стоимость опциона (которая при этом может составлять весьма существенную часть его стоимости).

Подход Core, Guay & Kothari (2002 г.)

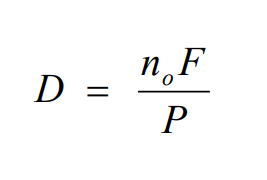
Еще более простая формула, и она же, вроде бы, решение проблемы, поскольку исследователи тоже опирались на внутреннюю стоимость опционов из предыдущего случая, просто поменяли ее на справедливую стоимость опциона и тем самым “ухватили” временную стоимость, которую подход в IAS 33 вообще игнорирует. Тем самым исследователям в 2002 году удалось учесть в расчете чуть больше эффектов разводнения. Казалось бы, уже неплохо – но лишь до определенного предела, ведь последующие эмпирические исследования показали, что только лишь половина всех эффектов разводнения находит свое отражение при использовании в расчете предложенной выше формулы – иначе говоря, с применением подхода “Treasury option method”.

Еще одна примечательная работа по этой теме датируется 2006 годом, но там речь идет не столько о расчетном методе, сколько о том, что именно по факту представляют собой опционы на акции работников: Landsman, Peasnell, Pope & Yeh утверждают, что их все следует на балансе отражать по статье обязательств, а в отчете о доходах - по справедливой стоимости. Тем самым они предложили простое решение проблемы различия между опционами, погашаемыми долевыми инструментами или же денежными средствами. Может быть даже слишком простое.

Улучшенный подход Van Zyl & Uliana

Как и в предыдущем случае, за основу авторы сегодняшней презентации взяли модель оценки Ольсона (Ohlson) 1995 г., дополнив ее адаптацией под опционы на акции работников в исполнении Hess & Lüders 2001 г. Альтернативная формула имеет вид:

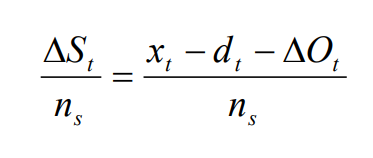
Первое, что важно отметить в предлагаемом новом подходе - это что, в отличие от предыдущих случаев, где производится корректировка знаменателя за счет изменения числа акций, здесь корректируется числитель, то есть сама прибыль. Корректировка прибыли происходит из-за изменения стоимости опционов.

Это несет с собой некоторые преимущества. Прежде всего, с точки зрения размытой прибыли на акцию, решается проблема различия между опционами, погашаемыми долевыми инструментами или же денежными средствами. Кроме того, ту же логику расчета можно легко применить к любым другим инструментам, ведь изменение их стоимости будет все так же учитываться по той же формуле. Тем самым решаются потенциальные проблемы, порождаемые тонкостями различия долевых и долговых инструментов в IFRS 9, или тем фактом, что какие-то инструменты стандарт учитывает по справедливой стоимости через прибыли и убытки, а другие при этом - нет.

Если сравнивать формулу с двумя предыдущими, какие их недостатки были устранены с новым подходом?

1. В подходе Core, Guay & Kothari 2002 г. действует допущение, что акционерная стоимость представляет собой линейную функцию от прибыли, тогда как рассматриваемый здесь улучшенный подход – более сложный, но благодаря этому отражает более сложные взаимосвязи между справедливой стоимостью и бухгалтерскими данными, которые нашли свое отражение в базовой модели Ольсона 1995 г. И еще в нем не решена проблема различных способах погашения опционов, долевыми инструментами или же денежными средствами, поскольку авторы этой проблемой даже не заморачивались.
2. Зато заморачивались Landsman, Peasnell, Pope & Yeh, но предложили слишком прямое, даже где-то примитивное решение проблемы, отнеся все опционы на акции работников к обязательствам. Это утверждение, по мнению авторов сегодняшнего подхода, весьма спорное. В конце концов, требования МСФО 2 по признанию (пп.7-9) ничего подобного не говорят, но к практике его применения никаких нареканий нет, стандарт вроде бы работает как надо и в переписывании не нуждается.
3. И в то же самое время, по утверждению авторов сегодняшнего подхода, все преимущества неплохой, в целом, модели Landsman, Peasnell, Pope & Yeh сохранены в том плане, что на уровне самого показателя разводненной прибыли на акцию их формула дает схожие результаты – зато не накладывает жесткого и нереалистичного ограничения по признанию инструментов.

Сопоставить три метода можно с помощью простой таблицы. Второй по счету столбец относится к рассматриваемому здесь улучшенному (предположительно) подходу, третий столбец – “традиционный” подход в IAS 33, а последний столбец отражает модель Core, Guay & Kothari, который выше еще был назван методом казначейских опционов (“Treasury Stock Method”). Сегодняшний подход, напоминаем, имеет альтернативное рабочее название “Метод корректировки прибыли”, поскольку чуть выше, сразу после первой демонстрации формулы, авторы прямо отметили основное отличие: корректируется именно прибыль, то есть числитель, а не число акций, которые стоят в знаменателе.

Далее, по второй строке приведенной ниже таблицы: корректировки в этом случае объясняются изменениями справедливой стоимости. В случае с традиционным подходом по IAS 33 речь идет об изменении внутренней стоимости опционов, ну а Core, Guay & Kothari смогли расширить это на справедливую стоимость.

Отдельная тема - услуги, подлежащие поставкам в будущем по условиям опциона на акции. Ни предлагаемый авторам подход, ни подход Core, Guay & Kothari этого не учитывает – в отличие от “классического”, где есть корректировка цены исполнения опциона, и это довольно любопытно. Авторы признаются, что не нашли весомых теоретических обоснований под требование, которое ввел в действие МСФО 2, потребовав корректировать цену исполнения на величину неамортизированных расходов, связанных с операциями, при которых работникам предоставляются опционы на акции.

Пример расчета

Чтобы лучше разобраться в логике, вероятно, стоить разобрать простенький гипотетический пример расчета на основе всех трех подходов. Предположим, у нас есть компания с денежным активом стоимостью 100, который генерирует доход в 10%, и 10 акциями в обращении. Если посмотреть на часть содержания ее отчета о доходах, то на протяжении двух отчетных периодов полученные доходы, доходы от оказанных услуг, рассчитанные по МСФО 2 расходы и, как итог, чистые доходы будут выглядеть следующим образом:

Величина EPS – прибыли на акцию – будет, таким образом, составлять 1,035 и 1,138 в эти два года. Что насчет размытой прибыли на акцию? Одной из отличительных черт сегодняшнего подхода является то, что он не игнорирует временную стоимость. Игнорирование временной стоимости имеет два недостатка: 1) Это означает игнорирование факта дисконтирования временной стоимости денег, а это одна из базовых концепций, и 2) Это означает игнорирование неопределенности, а нам известно, что чем больше неопределенность, тем выше временная стоимость.

Полученное значение разводненной прибыли на акцию будет отличаться лишь с подходом IAS 33, что объясняется тем фактом, что в нем игнорируется временная стоимость денег.

Усложним пример, добавив сюда фактор неопределенности после окончания первого отчетного периода. Процентный доход во втором отчетном периоде с равной вероятностью может принять разные значения. Неопределенность означает увеличение стоимости опционов и, как следствие, перемещение стоимости от акционеров к держателям опционов на акции.

Предлагаемый авторами подход скорректированной прибыли из всех трех лучше всего учитывает собой изменение стоимости для действующих акционеров. Интересно, что при этом подход Core, Guay & Kothari тоже не стоит совсем списывать со счетов, поскольку тот неплохо справляется с прогнозированием будущей прибыли. А вот подход IAS 33 из всех трех оказывается самым слабым. И действительно - практические расчеты на примере пяти реально существующих компаний в исполнении авторов показали, что из всех трех именно подход IAS 33 сильнее всего недооценивает величину размытия.