Продолжение данной статьи – CCF – лучшая альтернатива NPV
При использовании традиционных методов измерения стоимости, игнорирующих при учете экономических рисков принцип субъективной асимметричности экономических оценок, часто возникают проблемы. Для принятия более рациональных управленческих решений целесообразнее использовать инновационные, более адекватные методы.
Метод чистой приведенной стоимости — NPV (net present value) в настоящее время является неотъемлемым атрибутом бесчисленного множе-ства финансовых вычислений. Он широко применяется во всем мире и при анализе эффективности инвестиционных проектов, и при оценке стоимости имущества и имущественных прав, и даже при отражении активов и обязательств в бухгалтерском учете. NPV, пожалуй, является одним из наиболее широко используемых в современной экономике методов. Авторитет метода столь велик, что мало кто решается подвергать сомнению и критически анализировать его теоретические основания и практические недостатки.
Вместе с тем, в экономике нет незыблемых истин. И зачастую осознание существенных недостатков «традиционной» методологии служит мощным толчком к созданию новых, более адекватных методов и моделей. Инновационные методологии позволяют лучше «заглянуть» в будущее и, следовательно, принимать более рациональные решения.
Справедливости ради следует отметить, что, несмотря на огромную популярность метода NPV, некоторые всемирно известные специалисты уже предрекают близкую кончину этого метода в его современном виде. Так, например, один из наиболее авторитетных специалистов в сфере оценки профессор Том Коупленд утверждает: «Теория выбора (многим она известна также под названием «метод реальных опционов» — прим. авт.) — это техника финансового анализа, которая, по моему мнению, полностью вытеснит метод чистой приведенной стоимости в течение следующих десяти лет. Причина состоит в том, что метод чистой приведенной стоимости имеет недостатки, проявляющиеся при оценке инвестиционных проектов».
В чем же видит недостатки метода NPV один из наиболее авторитетных мировых специалистов в сфере оценки Том Коупленд: «Типичные недостатки метода чистой приведенной стоимости можно увидеть при анализе инвестиционного проекта сроком на 10 лет. Допустим, имеются прогнозы ожидаемого роста доходов и ожидаемых затрат. Они позволяют определить объемы чистых денежных потоков за вычетом текущих активов и капитальных затрат. Затем вы дисконтируете чистые денежные потоки на средневзвешенную стоимость капитала и вычитаете сумму первоначальных инвестиционных затрат. Если полученное значение будет больше нуля, то проект имеет положительную чистую приведенную стоимость, и вы можете принять его. Однако проблема заключается в том, что менеджеры, принимающие такие решения, знают, что при этом приходится полагаться на допущения, которые могут быть очень жесткими и даже неверными. Например, если вы принимаете участие в проекте, который реализуется с трудом, то он может 10 лет и не просуществовать, его или свернут, или значительно урежут. Если же проект окажется успешным, то его либо продлят, либо расширят. И, наконец, никто не говорит, что первоначальные инвестиции нужно делать сразу. Их иногда требуется делать через год, а то и через два. В этом случае уже возникает проблема отложенного выбора. Любой менеджер знает, что для каждого проекта всегда существует вероятность его свертывания, расширения или задержки. Все опытные менеджеры когда-либо оказывались в ситуациях, при которых им приходилось рассчитывать чистую приведенную стоимость, а затем отказываться от этих данных, так как их интуиция говорила им, что гибкий подход позволит увеличить стоимость проекта. Если смотреть на данный вопрос в таком ракурсе, то вы поймете всю ограниченность метода чистой приведенной стоимости».
Мы видим, что основным недостатком метода NPVТОМ Коупленд считает отсутствие гибкости, невозможность полноценного анализа сценариев, реально существующих при реализации большинства инвестиционных проектов. И способом устранения этого ключевого, по его мнению, недостатка является своеобразный синтез дерева решений (decision tree) и NPV, который, по сути, и представляет собой ядро метода реальных опционов (real option). Том Коупленд обращает внимание: «В академических кругах формируется мнение о том, что такой подход является единственным верным подходом к принятию инвестиционных решений, а метод чистой приведенной стоимости представляет лишь частный случай в рамках общей теории выбора».
Является ли метод реальных опционов достойной альтернативой методу NPV, исключающей его недостатки? Нет. Именно к такому выводу мы пришли в результате нашей многолетней практической деятельности и научных исследований.
В аспекте решения проблемы негибкости метода NPV, метод реальных опционов, безусловно, является революционным прорывом. Однако он не только не устраняет других, не менее существенных недостатков метода NPV, но иногда даже усугубляет их. Раскрытию некоторых из этих ключевых недостатков метода NPV посвящена наша статья. Мы говорим «некоторых», потому что изложить все ключевые недостатки указанного метода в одной статье не представляется возможным.
Итак, приступим к рассмотрению этих недостатков. Начнем с рассмотрения формулы чистой приведенной стоимости NPV для условий отсутствия неопределенности. Существуют различные ее варианты, однако, по сути, все они аналогичны:
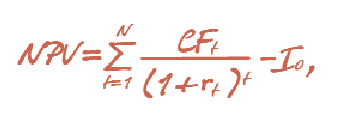
где I0 — первоначальные инвестиции, CFt — чистый поток средств в год t, rt — годовая ставка дисконта в год t, N — период прогнозирования.
Следует отметить, что различные авторы используют различные символьные обозначения параметров формулы NPV, а также их наименования. Практика свидетельствует, что различия наименований большинства параметров формулы NPVчаще всего носят чисто стилистический характер, и позиции различных специалистов в отношении их трактовки, как правило, совпадают. В отношении же параметра, соответствующего символу r в формуле (1), позиции различных специалистов не столь схожи и использование различных наименований этого параметра зачастую отражает различные подходы к его определению. Так, например, некоторые авторы определяют указанный параметр в достаточно общем виде как «ставку дисконтирования» или как «норму дисконта», другие же самим наименованием этого параметра указывают на механизм его расчета, определяя его как «стоимость капитала», или как «необходимую норму прибыли». Однако мы временно отложим подробное изучение теоретических оснований механизма дисконтирования в формуле NPV, поскольку оно требует особого внимания и тщательности рассмотрения, а пока сосредоточимся на сущности метода NPV.
Сущность NPV достаточно точно характеризуют слова известных специалистов доктора Джая Шима и доктора Джойла Сигела: «С помощью методов, основанных на чистой текущей (приведенной) стоимости, текущая стоимость будущих денежных потоков, ожидаемых по проекту, сравнивается с начальным объемом инвестированных средств. Чистый денежный поток — это разность между прогнозируемым притоком денежных средств, генерируемым в результате инвестиций в проект, и ожидаемым оттоком денежных средств. В качестве ставки дисконтирования следует использовать минимальную норму прибыли на инвестированный капитал, установленную компанией».
Представив чистый денежный поток как разницу между притоком и оттоком денежных средств, формулу NPV можно зафиксировать в следующем виде:
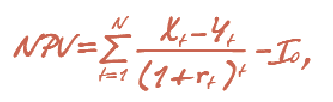
где Xt — приток денежных средств в год t, Yt — отток денежных средств в год t
При этом, следует обратить внимание, что, по сути, первоначальные инвестиции I0 являются оттоком денежных средств в год t = 0.
Хотя формулы (1) и (2) математически эквивалентны, однако, «развернутая» форма метода NPV (2) имеет особое прикладное значение, что будет наглядно продемонстрировано на конкретных примерах, представленных ниже.
Рассмотрев сущность базовой формулы NPV, перейдем в нашем анализе от идеального варианта — отсутствия неопределенности к реальным условиям, в которых таковая имеет место и, безусловно, должна учитываться.
Как правило, неопределенность проявляется в вероятностном характере будущих событий, определяющих стоимость положительных и отрицательных денежных потоков, отражаемых в числителе формулы NPV, а также в наличии экономических рисков, присущих этим потокам. Как же метод NPV справляется с учетом этих факторов реального экономического мира?
Прежде чем перейти непосредственно к поиску ответа на этот вопрос, обратим ваше внимание на несколько ключевых моментов, связанных с сущностью понятий «вероятность» и «экономический риск».
Вероятность события, по сути, представляет собой возможность его наступления и характеризуется числовым значением, находящимся в диапазоне [0; 1]. Вероятность события, равная 0, указывает на невозможность его наступления, а вероятность события, равная 1, указывает на то, что оно обязательно наступит. Таким образом, для того чтобы определить стоимость денежного потока с учетом вероятности его возникновения, достаточно умножить величину позитивного или негативного денежного потока на соответствующее значение вероятности: Хрх или Ypr Однако далеко не так просто и однозначно обстоит дело с учетом экономических рисков. В этом вопросе сложности возникают уже на этапе концептуальной интерпретации этого понятия.
С первых шагов специалист, постигающий азы рискологии, сталкивается с трактовкой экономического риска, подобной той, которую предлагает один из наиболее авторитетных в мире специалистов в области оценки Асват Дамодаран: «…риск определяется преимущественно с помощью терминов, имеющих негативный оттенок. В финансовой сфере риск понимается по-иному и несколько шире. С точки зрения финансиста риск означает вероятность того, что доход на сделанную инвестицию будет отличаться от ожидаемого. Таким образом, риск включает в себя не только неблагоприятные (доходы ниже ожидаемых), но и благоприятные (доходы выше ожидаемых) исходы. На практике, первый вид риска можно назвать «риск снижения» (downside risk), а второй вид — «риск повышения» (upside risk), и при измерении риска мы будем учитывать оба этих вида». Следует обратить внимание, что многие специалисты воспринимают такой подход, чуть ли не как азбучную истину.
Наши исследования наглядно продемонстрировали ошибочность мнения о том, что экономический риск необходимо трактовать и как возможность отклонения прогнозируемой величины денежного потока в положительном направлении. Кстати, известные российские специалисты П.Л. Виленский, В.Н. Лившиц, С.А. Смоляк также отмечают, что «Трактовка риска как любых, а не только негативных отклонений, типична для большинства западных ученых и специалистов». В процессе наших исследований мы последовательно пришли к тому, что экономический риск необходимо трактовать как вероятное уменьшение стоимости положительных CCF (условно-денежных потоков) будущих периодов и вероятное увеличение (по абсолютной величине) стоимости отрицательных CCF будущих периодов, происходящие вследствие наступления событий, нежелательных для конкретного субъекта экономических отношений [1 -3].
То есть, для положительных денежных потоков экономический риск состоит в том, что они могут оказаться меньше прогнозируемых, а для отрицательных денежных потоков — в том, что их значения могут превысить прогнозируемую величину. Возможность того, что положительные денежные потоки окажутся выше прогнозируемых, а отрицательные денежные потоки — ниже прогнозируемых, вовсе не является экономическим риском!
Признание этого принципиального вывода изначально избавляет нас от необходимости рассмотрения целого класса подходов к учету экономических рисков, основанных на использовании показателей вариации, таких как дисперсия, среднеквадратиче-ское отклонение, коэффициент вариации и т. п. Ведь хотя они в некоторых случаях являются достаточно подходящими характеристиками неопределенности, но ни один из них в достаточной мере не соответствует сущности понятия «экономический риск».
Среди основных подходов к учету экономических рисков в рамках метода NPVможно выделить следующие:
- Учет экономических рисков в знаменателе формулы NPV посредством корректировки ставки дисконта.
- Учет экономических рисков в числителе формулы NPVпосредством корректировки чистых денежных потоков.
- Учет экономических рисков как в числителе формулы NPV путем корректировки чистых денежных потоков, так и в ее знаменателе корректировкой ставки дисконта.
Кратко охарактеризуем указанные подходы и проанализируем экономическую корректность каждого из них.
Учет экономических рисков в знаменателе формулы NPV посредством корректировки ставки дисконта. Данный подход считается одним из основных в современной практике и основывается на следующем суждении: «Чем выше инвестор оценивает риск проекта, тем более высокие требования он предъявляет к его доходности. В расчетах это отражается путем увеличения нормы дисконта — включения в нее поправки на риск (премии за риск)».
Данный подход в общем виде можно отразить следующей формулой:
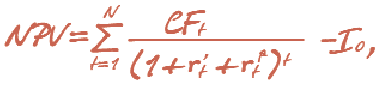
где rt’ — безрисковая годовая ставка дисконта в год t, r* — премия за риск в год t
Разность величин NPV без учета экономического риска и с его учетом в условиях данного подхода можно выразить следующим образом:

Этот подход ошибочно воспринимается многими специалистами как универсальный механизм учета рисков в условиях неопределенности. Так, например, профессор Ченг Ли и профессор Джозеф Финнерти указывают: «Хотя во многих реальных ситуациях у нас есть некие возможности для оценки величины будущих поступлений, эти оценки никогда не бывают достаточно точными. На практике необходимо принимать в расчет некоторую долю риска. Для этого мы дисконтируем будущие положительные денежные потоки по ставке гр которая в данном случае является ставкой для некоторых эквивалентных по риску ценных бумаг или инвестиций. В принципе этого достаточно, чтобы подсчитать приведенную стоимость сколь угодно рискованного вложения».
Однако не все специалисты придерживаются такой точки зрения. Так, например, П. Л. Виленский, В. Н. Лившиц и С. А. Смоляк сопровождают рассмотрение данного подхода следующим критическим комментарием: «Такой способ широко рекомендуется в западной финансовой литературе и часто используется в практических расчетах. Однако он не является ни единственно возможным, ни достаточно хорошо теоретически обоснованным». Не осуществляя анализ теоретических оснований этого подхода, в данной статье на примерах мы продемонстрируем его практическую несостоятельность.
Рассмотрим первый пример, приведенный в табл. 1. Обратим внимание на строку «Разность приведенной стоимости чистых денежных потоков без учета и с учетом риска». Каждая величина в этой строке вычисляется как разность соответствующих значений двух предыдущих строк: приведенной стоимости чистых денежных потоков (без учета риска — PVt’) и приведенной стоимости чистых денежных потоков (c учетом риска — PVt).
Табл.1. Расчет NPV с учетом риска в знаменателе (посредством корректировки ставки дисконта)
| Годы | 0 | 1 | 2 | 3 | 4 | 5 |
| Первоначальные инвестиции (I 0), тыс . у . е . | 3000 | |||||
| Безрисковая годовая ставка дисконта r t ', % | 10 | 10 | 10 | 10 | 10 | |
| Премия за риск r t p, % | 5 | 5 | 5 | 5 | 5 | |
| Годовая ставка дисконта с учетом премии за риск r f + r t p , % | 15 | 15 | 15 | 15 | 15 | |
| Положительные денежные потоки ( Xt ), тыс . у . е . | 2 900 | 4 500 | 4 200 | 1 500 | 500 | |
| Отрицательные денежные потоки (Y t), тыс . у . е . | 1 800 | 2 300 | 2 200 | 1 900 | 1 500 | |
| Чистые денежные потоки ( CF t ), тыс . у . е . | 1 100 | 2 200 | 2 000 | – 400 | – 1 000 | |
| Приведенная стоимость чистых денежных потоков ( без учета риска ) PV t ', тыс . у . е . | 1 000 | 1 818 | 1 503 | – 273 | – 621 | |
| Приведенная стоимость чистых денежных потоков ( с учетом риска ) PVt , тыс . у . е . | 957 | 1 664 | 1 315 | – 229 | – 497 | |
| Разность приведенной стоимости чистых денежных потоков без учета и с учетом риска[ DPV t ) f тыс . у . е . | 43 | 154 | 188 | – 44 | – 124 | |
| Чистая приведенная стоимость ( NPV ) с учетом риска , тыс . у . е . | 210 |
В первые три года величины разности приведенной стоимости чистых денежных потоков без учета и с учетом риска (DPVt) положительны и равны, соответственно, 43, 154 и 188 тыс. у. е. Но что же означают отрицательные значения DPVt в 4 – и 5-й годы, составившие, соответственно, – 44 и – 124 тыс. у. е.?! Почему учет риска уменьшает дисконтированные отрицательные денежные потоки проекта по абсолютной величине? Получается, что чем выше премия за риск, тем меньшее влияние оказывают отрицательные денежные потоки на NPV. Вводя в ставку дисконта премию за риск, мы уменьшаем величину NPV за счет положительных значений ДPVt в первые 3 года реализации проекта в целом на 385 тыс. у. е. (43 тыс. у.е. + 154 тыс. у. е. + 188 тыс. у. е.). Но ведь вместе с тем, введением премии за риск мы также увеличиваем значение NPV на 168 тыс. у. е. за счет отрицательной величины DPVt в 4 – и 5-й годы [ – 44 тыс. у. е. + ( – 124 тыс. у. е.)]. Разве таким образом мы корректно учитываем экономический риск? Ведь уменьшение отрицательных денежных потоков по абсолютной величине это, по сути, выигрыш, а не риск!
Табл.2. Расчет NPV с учетом риска в знаменателе (премия за риск rf принята равной 0%)
| Годы | 0 | 1 | 2 | 3 | 4 | 5 |
| Первоначальные инвестиции (I 0), тыс . у . е . | 200 | |||||
| Безрисковая годовая ставка дисконта r t ', % | 10 | 10 | 10 | 10 | 10 | |
| Премия за риск r t p, % | 0 | 0 | 0 | 0 | 0 | |
| Годовая ставка дисконта с учетом премии за риск r f + r t p , % | 10 | 10 | 10 | 10 | 10 | |
| Положительные денежные потоки ( Xt ), тыс . у . е . | 3 300 | 2 750 | 2 650 | 2 600 | 2 525 | |
| Отрицательные денежные потоки (Y t), тыс . у . е . | 2 500 | 3 500 | 2 600 | 2 550 | 2 500 | |
| Чистые денежные потоки ( CF t ), тыс . у . е . | 800 | – 750 | 50 | 50 | 25 | |
| Приведенная стоимость чистых денежных потоков ( без учета риска ) PV t ', тыс . у . е . | 727 | – 620 | 38 | 34 | 16 | |
| Приведенная стоимость чистых денежных потоков ( с учетом риска ) PVt , тыс . у . е . | 727 | – 620 | 38 | 34 | 16 | |
| Разность приведенной стоимости чистых денежных потоков без учета и с учетом риска ( DPV ,), тыс . у . е . | 0 | 0 | 0 | 0 | 0 | |
| Чистая приведенная стоимость ( NPV ), тыс . у . е . | – 5 |
Рассмотрим еще пример (см. табл. 2). Из этого примера видно, что премия за риск rt принята равной 0%, а чистая приведенная стоимость NPV оказалась отрицательной: – 5 тыс. у. е. В соответствии со стандартными правилами метода NPV такой инвестиционный проект следует отвергнуть. Тем более, что в этом проекте даже не учтен риск.
А как бы изменилась оценка проекта, если бы мы учли риск, приняв премию за риск rtp равной 9%? Большинство участников наших специальных семинаров «Оценка инвестиционных проектов на базе концепции CCF», опираясь на здравый смысл, отвечают, что оценка инвестиционного проекта, безусловно, ухудшилась бы — отрицательное значение NPV стало бы еще больше по абсолютной величине. Представьте их удивление, когда они обнаруживают, что при введении в указанном примере премии за риск, NPVне только не «уходит глубже в минус», но даже выходит в зону положительных значений! То есть оценка проекта меняется не только количественно, но и качественно — теперь его целесообразно не отвергнуть, а принять, поскольку его NPV положительна и составляет 7 тыс. у. е. (см. табл. 3).
Табл.3. Расчет NPV с учетом риска в знаменателе (премия за риск rtp принята равной 9%)
| Годы | 0 | 1 | 2 | 3 | 4 | 5 |
| Первоначальные инвестиции (I 0), тыс.у.е. | 200 | |||||
| Безрисковая годовая ставка дисконта r t ', % | 10 | 10 | 10 | 10 | 10 | |
| Премия за риск rtp, % | 9 | 9 | 9 | 9 | 9 | |
| Годовая ставка дисконта с учетом премии за риск r t '+ rtp , % | 19 | 19 | 19 | 19 | 19 | |
| Положительные денежные потоки ( X t ), тыс.у.е. | 3 300 | 2 750 | 2 650 | 2 600 | 2 525 | |
| Отрицательные денежные потоки ), тыс.у.е. | 2 500 | 3 500 | 2 600 | 2 550 | 2 500 | |
| Чистые денежные потоки ( CF t ), тыс.у.е. | 800 | – 750 | 50 | 50 | 25 | |
| Приведенная стоимость чистых денежных потоков ( без учета риска ) PV t ', тыс.у.е. | 727 | – 620 | 38 | 34 | 16 | |
| Приведенная стоимость чистых денежных потоков ( с учетом риска ) PV t , тыс.у.е. | 672 | – 530 | 30 | 25 | 10 | |
| Разность приведенной стоимости чистых денежных потоков без учета и с учетом риска[ DPV t ) f тыс. у.е. | 55 | – 90 | 8 | 9 | 6 | |
| Чистая приведенная стоимость ( NPV ) с учетом риска , тыс.у.е. | 7 |
Как видно из табл. 3, учет премии за риск приводит к тому, что величина DPVP отражающая экономический риск, во 2-й год приобретает столь значительное отрицательное значение ( – 90), что по модулю оказывается больше суммы всех положительных значений DPVt в остальные годы (55 + 8 + 9 + 6 = 78 тыс. у. е.). Таким образом, в данном примере введение премии за риск не только не позволило учесть экономический риск проекта, а даже привело к повышению его инвестиционной привлекательности!
Как мы уже отмечали, мы не единственные, кто обнаружил указанные недостатки рассматриваемого подхода. П.Л. Виленский, В.Н. Лившиц и С.А. Смоляк в результате рассмотрения подобных ситуаций заключают: «Итак, мы приходим к выводу, что при наличии вероятностной неопределенности влияние факторов риска отнюдь не всегда может быть отражено включением в норму дисконта премии за риск. Более того, в отдельных ситуациях адекватный учет неопределенности требует не увеличения, а уменьшения нормы дисконта».
Рассматривая данный подход к учету экономического риска при расчете NPV, П.Л. Виленский, В.Н. Лившиц и С.А. Смоляк приходят к выводу, что если его и можно использовать, то с учетом ряда особых условий: использования дифференцированной по годам с учетом наличия конкретных факторов риска, а не единой для всего проекта ставки дисконта; использования различных ставок дисконта для лет, в которые чистый денежный поток отрицателен и для лет, в которые он положителен, причем с той особенностью, что для отрицательных денежных потоков премия за риск должна быть отрицательной или нулевой.
Однако результаты наших исследований свидетельствуют, что даже учет этих непростых для практической реализации требований вовсе не обеспечит адекватных результатов!
Дабы не быть голословными, приведем пример (табл. 4). Для этого воспользуемся рекомендацией П.Л. Виленского, В.Н. Лившица и С А. Смоляка: «мы уже отмечали, что отражать в норме дисконта имеет смысл только риск неполучения доходов. Поэтому вводить премию за риск на этапе осуществления инвестиций нецелесообразно. Более того, это нецелесообразно и тогда, когда, неважно по каким причинам, денежный поток по проекту отрицателен (расходы превышают денежные поступления)».
Таьл.4. Расчет NPV с учетом риска в знаменателе (премия за риск rt для положительных чистых денежных потоков принята равной 5%, для отрицательных — принята равной 0%)
| Годы | 0 | 1 | 2 | 3 | 4 | 5 |
| Первоначальные инвестиции (I 0), тыс . у . е . | 3000 | |||||
| Безрисковая годовая ставка дисконта r t', % | 10 | 10 | 10 | 10 | 10 | |
| Премия за риск rtp, % | 5 | 5 | 5 | 0 | 0 | |
| Годовая ставка дисконта с учетом премии за риск r t' + rtp , % | 15 | 15 | 15 | 10 | 10 | |
| Положительные денежные потоки ( X t ), тыс . у . е . | 2 900 | 4 500 | 4 200 | 1 500 | 500 | |
| Отрицательные денежные потоки (Y t), тыс . у . е . | 1 800 | 2 300 | 2 200 | 1 900 | 1 500 | |
| Чистые денежные потоки ( CF t ), тыс . у . е . | 1 100 | 2 200 | 2 000 | – 400 | – 1 000 | |
| Приведенная стоимость чистых денежных потоков ( без учета риска ) PV t ', тыс . у . е . | 1 000 | 1 818 | 1 503 | – 273 | – 621 | |
| Приведенная стоимость чистых денежных потоков ( с учетом риска ) PVt , тыс . у . е . | 957 | 1 664 | 1 315 | – 273 | – 621 | |
| Разность приведенной стоимости чистых денежных потоков без учета и с учетом риска ( DPV t ), тыс . у . е . | 43 | 154 | 188 | 0 | 0 | |
| Чистая приведенная стоимость ( NPV ) с учетом риска , тыс . у . е . | 42 |
Дабы не быть голословными, приведем пример (табл. 4). Для этого воспользуемся рекомендацией П.Л. Виленского, В.Н. Лившица и С А. Смоляка: «мы уже отмечали, что отражать в норме дисконта имеет смысл только риск неполучения доходов. Поэтому вводить премию за риск на этапе осуществления инвестиций нецелесообразно. Более того, это нецелесообразно и тогда, когда, неважно по каким причинам, денежный поток по проекту отрицателен (расходы превышают денежные поступления)».
Для формирования примера (табл. 4), воспользуемся данными табл 1. Заменим 5%-ную премию за риск в 4 – и 5-м годах, в которых чистый денежный поток отрицателен, на 0%-ную. В результате мы получили NPV, равную 42 тыс. у. е., вместо NPV, равной 210 тыс. у. е. (см. табл. 1).
Однако попытка «залатать дыры» неадекватного подхода к учету экономических рисков в формуле NPV, путем изощренной корректировки ставок дисконта, на поверку оказывается весьма опасной иллюзией разрешения проблем! Ведь «обнулив» премию за риск для 4 – и 5-го годов, в которых чистый денежный поток оказывается отрицательным, мы совершенно не учитываем, что он, в свою очередь, складывается из отрицательных и положительных денежных потоков, каждому из которых присущи свои риски, которые в результате оказываются вовсе неучтенными! То есть, руководствуясь данным подходом, в те годы, в которых чистый денежный поток оказывается отрицательным, мы не учитываем ни экономических рисков, присущих отрицательным денежным потокам, ни экономических рисков, присущих положительным денежным потокам!
Так например, чистый денежный поток 4-го года: – 400 тыс. у. е. складывается из положительного денежного потока 1 500 тыс. у. е. и отрицательного денежного потока 1 900 тыс. у. е., а чистый денежный поток 5-го года: – 1 000 тыс. у. е. является результатом положительного денежного потока 500 тыс. у. е. и отрицательного денежного потока 1 500 тыс. у. е. Учитываем ли мы, применяя нулевую премию за риск, что притоки 4 – и 5-го годов: 1 500. и 500 тыс. у. е. могут оказаться меньшими, чем предполагалось? И как нулевая премия за риск учитывает то, что оттоки 4 – и 5-го годов: 1 900 тыс. у. е. и 1 500 тыс. у. е. могут оказаться большими, чем прогнозировалось? Очевидно, никак!
Более того, даже используя премию за риск для положительных чистых денежных потоков (в примере, представленном в табл. 4, это годы 1-3), мы ведь, по сути, дисконтируем с поправкой на риск и положительные и отрицательные денежные потоки, формирующие чистые денежные потоки. Таким образом, мы снова сталкиваемся с проблемой, обнаруженной в примере, представленном в табл. 1, только теперь она проявляется «внутри» чистых денежных потоков соответствующих лет.
Кроме того, даже если попытаться принимать ставки дисконта индивидуально для каждого отдельно взятого денежного потока, то будет весьма нелегко находить необходимый диапазон корректировок и объяснять их взаимосвязь с денежными суммами потенциальных потерь, которые, в конечном счете, и характеризуют экономические риски. Ведь какой бы абстрактной не была идея экономического риска в теории, в каждой конкретной практической ситуации в расчетах он должен получать вполне определенное денежное выражение! В наших исследованиях мы показали, что экономические риски должны исчисляться не безразмерными величинами, а суммами денежных средств [1-3].
Завершая анализ первого подхода к учету экономических рисков, необходимо отметить, что совершенно неясно как при этом подходе учитывается вероятность денежных потоков и учитывается ли она вообще? Положениями принципа субъективной асимметричности экономических оценок нами зафиксированы различия в учете экономических рисков и вероятностей, поэтому отсутствие ответа на вопрос о способе учета вероятности в рамках рассмотренного подхода также является весьма серьезным аргументом не в его пользу
Чем детальнее мы изучали механизм учета экономических рисков в знаменателе формулы NPV, варьируя значения ставки дисконта, тем увереннее приходили к выводу о том, что это как раз тот случай, когда математика и экономика расходятся как поезда по параллельным путям. То есть, изменяя ставку дисконта, мы, безусловно, влияем на конечную величину NPV, и порой это влияние даже кажется нам правдоподобным: выше ставка — меньше NPV, и наоборот. Но, как показывал осуществленный нами анализ, это лишь иллюзия адекватности.
Итак, получение адекватного результата при учете экономических рисков в знаменателе формулы NPV посредством корректировки ставки дисконта — это скорее счастливое исключение, чем верное правило.
Недостатки других подходов к учету экономических рисков в рамках метода NPV будут рассмотрены в следующих номерах журнала.

