Материал является продолжением статьи «Метод NPV: фундаментальные недостатки» (см. «Финансовый директор».— 2005.—№2). На конкретных примерах продолжим демонстрацию проблем, возникающих при использовании традиционных методов измерения стоимости, игнорирующих при учете экономических рисков принцип субъективной асимметричности экономических оценок.
Учет экономических рисков в числителе формулы NPV посредством корректировки чистых денежных потоков. Данный подход широко известен специалистам. Например, профессор Ченг Ли и профессор Джозеф Финнерти указывают: «Мы показали, что когда приходится иметь дело с риском проекта или финансового актива, его можно учесть, изменив знаменатель, т. е. ставку дисконтирования, в уравнении оценки. При этом большему риску соответствует более высокая ставка дисконтирования. Но риск можно учесть и за счет изменения числителя в уравнении приведенной стоимости, т. е. за счет изменения потока данных средств». Наглядной иллюстрацией подхода может служить метод безрискового эквивалента (certainty equivalent method).
В общем виде его можно отразить следующей формулой:
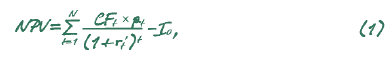
Разность величин NPV без учета экономического риска и с его учетом в условиях данного подхода можно выразить следующим образом:
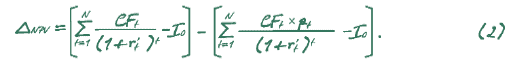
Заметным отличием такого подхода от учета экономических рисков в знаменателе формулы NPV посредством корректировки ставки дисконта является то, что он явно учитывает вероятности. Из формул 1 и 2 следует, что механизм учета вероятностей при данном подходе одновременно играет роль и механизма учета экономических рисков. Однако насколько оправдана такая концепция? Для наглядности рассмотрим ее на примере (табл. 1).
| 0 | 1 | 2 | 3 | 4 | 5 | |
| Первоначальные инвестиции (I0), тыс. у.е. | 3000 | |||||
| Безрисковая годовая ставка дисконта rt', % | 10 | 10 | 10 | 10 | 10 | |
| Положительные денежные потоки (Xt), тыс. у.е. | 2900 | 4500 | 4200 | 1500 | 500 | |
| Отрицательные денежные потоки (Yt), тыс. у.е. | 1800 | 2300 | 2200 | 1900 | 1500 | |
| Чистые денежные потоки ( CFt ), тыс. у.е. | 1100 | 2200 | 2000 | – 400 | – 1 000 | |
| Вероятность возникновения чистых денежных потоков (pt) | 0,9 | 0,9 | 0,9 | 0,9 | 0,9 | |
| Стоимость денежных потоков с учетом вероятности (CFt * pt), тыс. у.е. | 990 | 1980 | 1800 | – 360 | – 900 | |
| Приведенная стоимость денежных потоков без учета вероятности их возникновения (PVt), тыс. у.е. | 1000 | 1818 | 1503 | – 273 | – 621 | |
| Приведенная стоимость денежных потоков с учетом вероятности их возникновения (PVt), тыс. у.е. | 900 | 1636 | 1352 | – 246 | – 559 | |
Разность приведенной стоимости чистых денежных потоков без учета и с учетом вероятности (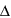 PVt), тыс. у.е. PVt), тыс. у.е. |
100 | 182 | 151 | – 27 | – 62 | |
| Чистая приведенная стоимость (NPV) с учетом риска , тыс. у.е. | 83 |
Обратившись к строке «Разность приведенной стоимости чистых денежных потоков без учета и с учетом вероятности» табл. 1, обнаруживаем в 4-и 5-м годах отрицательные значения этой разности. Очевидно, что в этих периодах, умножив величины чистых денежных потоков на соответствующие значения вероятности, не только не учтен присущий им экономический риск, а наоборот, учтен некий дополнительный выигрыш. Разве можно назвать риском уменьшение отрицательного денежного потока 4-го года с 400 до 360 тыс. у. е.?! И можно ли считать, что учтен риск в 5-м году, если вместо «безрисковой» величины отрицательного денежного потока 1 000 тыс. у. е., в расчетах NPV используется отрицательный денежный поток, равный 900 тыс. у. е. с учетом риска. Итак, снова математика подхода безупречна, а экономика оставляет желать лучшего!
Кому-то может показаться, что эта проблема носит частный характер, и просто выбран «неудачный пример» с отрицательными чистыми денежными потоками. Но в таком случае давайте отбросим 4 – и 5-й годы, и рассмотрим насколько адекватно данный подход учитывает вероятности и риски для периодов с положительными чистыми денежными потоками (1-3 годы).
На первый взгляд, умножением чистых денежных потоков на соответствующие им величины вероятностей, удалось учесть как вероятности, так и риски для денежных потоков, ведь величина экономического риска для чистых денежных потоков в 1-, 2-и 3-м годах положительна. Но это лишь на первый взгляд.
Не следует забывать, что чистый денежный поток — это расчетный показатель, определяемый разностью положительных и отрицательных денежных потоков. С учетом этого очевидного положения ситуация предстает в качественно ином виде. Применяя определенный коэффициент вероятности к чистому денежному потоку (CFt), по сути, применяем его к обеим составляющим этого параметра: как к положительному (Xt), так и отрицательному денежному потоку (Yt). То есть, в рассматриваемом примере, умножаем на 0,9 как положительные (2 900 х 0,9 = 2 610; 4 500 х 0,9 = 4 050; 4 200 х 0,9 = 3 780;…), так и отрицательные денежные потоки (1 800 х 0,9 = 1 620; 2 300 х 0,9 = 2 070; 2 200 х 0,9 = 1 980;…). Казалось бы, зачем представлять в развернутом виде расчет чистых денежных потоков с учетом вероятностей, ведь это не влияет на результат расчета? Однако этот прием позволяет продемонстрировать фундаментальный недостаток рассматриваемого подхода к учету экономических рисков.
Практики, конечно же, понимают, что вероятности возникновения положительных и отрицательных денежных потоков, как правило, различны. Причем в случае добросовестного ведения бизнеса отрицательные денежные потоки, обычно, более «гарантированны», чем положительные денежные потоки. Однако этот нюанс может быть с легкостью учтен введением различных значений вероятности для положительных и отрицательных денежных потоков. Фундаментальная же проблема состоит совершенно в другом, и ее нельзя решить в рамках данного подхода никакой дифференциацией значений вероятности для положительных и отрицательных денежных потоков.
Поскольку вероятность ни при каких условиях не может превышать единицы, а в условиях неопределенности всегда меньше ее, то умножение положительных денежных потоков на величину соответствующей вероятности позволяет учесть как вероятности, так и экономические риски. Ведь, как уже неоднократно показывалось, для положительных денежных потоков экономический риск заключается в том, что они могут оказаться меньше прогнозируемых, и, соответственно, коэффициент вероятности, меньший единицы, позволяет учесть этот риск.
Что же касается отрицательных денежных потоков, то, умножая их на соответствующие величины вероятностей, которые в условиях неопределенности всегда меньше единицы, уменьшаем по абсолютной величине значения этих отрицательных денежных потоков. Таким образом, учитывая вероятность их возникновения, отнюдь не учитываем присущие им экономические риски. Именно в этом и состоит фундаментальная проблема данного подхода. Ведь, как уже отмечалось, экономический риск для отрицательных денежных потоков заключается не в том, что они могут оказаться меньше прогнозируемых, а в том, что они могут оказаться больше, чем планировалось! Из рассматриваемого примера, следует, что «безрисковые» отрицательные денежные потоки первых трех лет (1 800, 2 300 и 2 200) оказываются выше этих же отрицательных денежных потоков с учетом риска: 1 620, 2 070 и 1 980. Можно ли назвать механизм, дающий такие результаты, способом адекватного учета экономических рисков?!
Учет вероятностей по отношению к отрицательным денежным потокам не приводит автоматически к учету присущих им экономических рисков при расчете NPV. Необходим специальный дополнительный учет экономических рисков для отрицательных денежных потоков. Это утверждение, отражающее идею принципа субъективной асимметричности экономических оценок, справедливо вовсе не для какого-то отдельно взятого примера, а для всех случаев, в которых имеет место неопределенность, придающая вероятностный и рисковый характер денежным потокам. Это достаточно наглядно продемонстрировано в работах [1-3]. Если же нет неопределенности, то нет и проблемы, поскольку можно смело использовать формулы NPV (см. «Финансовый директор».— 2005.— № 2) без учета каких-либо вероятностей или рисков. Однако специалисты прекрасно понимают, что реальный мир неразрывно связан с неопределенностью, и учетом ее последствий пренебрегать нельзя.
Изложенное наглядно свидетельствует, что этот подход не позволяет адекватно учитывать вероятности и экономические риски денежных потоков при определении чистой приведенной стоимости NPV. Строго говоря, метод NPV справляется с задачей учета экономических рисков лишь в одном случае — в случае их отсутствия.
Следует особо подчеркнуть, что принцип субъективной асимметричности экономических оценок является универсальным и указывает на некорректность учета вероятностей и экономических рисков посредством умножения чистых, итоговых потоков на соответствующие величины вероятностей, не только в случае применения метода NPV, но и в случае использования метода реальных опционов.
Не будем вдаваться в подробности механизма работы модели реальных опционов, которая, по словам Тома Коупленда, Тима Коллера и Джека Муррина «сочетает в себе наилучшие черты и метода чистой приведенной стоимости, и анализа «дерева решений». Однако отметим, что эта модель, так же как и метод NPV, предусматривает применение коэффициентов вероятности к чистым потокам (интегральным эффектам) ветвей дерева решений. А это, как и в случае с методом NPV, противоречит принципу субъективной асимметричности экономических оценок, и существенно искажает результаты измерения стоимости в условиях неопределенности!
Игнорирование объективной природы принципа субъективной асимметричности экономических оценок и умножение чистых денежных потоков на коэффициенты вероятности в рамках метода NPV или метода реальных опционов, по сути, означает отказ от учета экономического риска, присущего отрицательным денежным потокам, что зачастую неоправданно завышает значения стоимости, полученные с использованием такого подхода.
Одновременный учет экономических рисков в числителе формулы NPV посредством корректировки чистых денежных потоков и в ее знаменателе посредством корректировки ставки дисконта. Этот подход довольно широко распространен на практике и является своеобразной комбинацией двух описанных ранее подходов. Так, например, Джай Шим и Джойл Сигел утверждают: «Риск может учитываться с помощью определения вероятностного денежного потока с применением вероятностей и ставки дисконтирования, устанавливаемой в зависимости от рискованности альтернативных проектов».
В общем виде это можно отразить с помощью формулы:
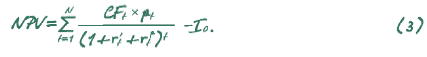
Разность величины NPVбез учета экономического риска и с его учетом можно выразить следующим образом:
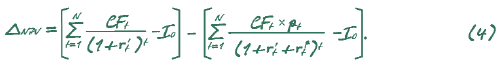
Для экономии времени, не станем рассматривать числовой пример, иллюстрирующий некорректность данного подхода. Симбиоз двух рассмотренных ранее подходов не только не обеспечивает возможности корректного учета вероятностей и экономических рисков денежных потоков, но и вовсе приводит к неадекватным результатам.
Так, например, П.Л. Виленский, В.Н. Лившиц, С.А. Смоляк, рассматривая пример использования данного подхода, со ссылкой на аналогичный пример известных финансистов Брейли и Майерса, утверждают: «На самом деле расчет неверен, ибо риск проекта учтен здесь дважды: при расчете ожидаемых (средних) денежных потоков и в норме дисконта».
Таким образом, данный подход также не позволяет адекватно учитывать вероятности и экономические риски денежных потоков при определении чистой приведенной стоимости NPV в условиях неопределенности.
Исходя из изложенного, можно констатировать, что наиболее широко применяемые методы измерения стоимости: метод NPV и метод реальных опционов, оказываются несостоятельными в вопросе учета вероятности и рисков денежных потоков в условиях неопределенности. Означает ли это тупик или толчок к развитию новой методологии, лишенной обнаруженных недостатков?
Лучшим свидетельством второй позиции являются предложенные «золотая формула CCF» и «платиновая формула CCF» (базирующиеся на концепции CCF — conventionally cash flows conception [3]), позволяющие корректно учитывать как вероятности, так и экономические риски при измерении стоимости в условиях неопределенности. Обе формулы базируются, в том числе, и на принципе субъективной асимметричности экономических оценок.
«Золотая формула CCF» имеет следующий вид:
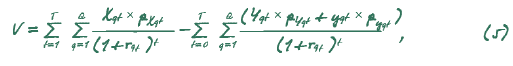
PXqt — вероятность возникновения соответствующего положительного условно-денежного потока в точке q в момент времени t, отражающая связанный с ним экономический риск;
Xqt*PXqt — величина положительного условно-денежного потока в точке q в момент времени t, с учетом вероятности его возникновения и присущего ему экономического риска;
Yqt — величина отрицательного условно-денежного потока в точке q в момент времени t;
PYqt — вероятность возникновения соответствующего отрицательного условно-денежного потока в точке q в момент времени t;
Yqt*PYqt — величина отрицательного условно-денежного потока в точке q в момент времени t, с учетом вероятности его возникновения;
yqt — величина дополнительного отрицательного условно-денежного потока в точке q в момент времени t, отражающего экономический риск, связанный с отрицательным условно-денежным потоком;
Pyqt — вероятность возникновения соответствующего дополнительного отрицательного условно-денежного потока в точке q в момент времени t, отражающего экономический риск, связанный с отрицательным условно-денежным потоком;
уqt*Pyqt— величина экономического риска, присущего отрицательному условно-денежному потоку в точке q в момент времени t;
rqt — безрисковая годовая ставка дисконта в точке q в момент t
Возможно, формула (5) имеет излишне громоздкий вид и визуально кажется более сложной, чем формула NPV. Однако это не более чем визуальный эффект, обусловленный стремлением к строгости описания ее параметров.
Столь громоздкий вид формуле (5) придает использование индексов q и t практически для всех параметров, а также соответствующее двойное суммирование, необходимое для свертки потоков в условиях использования этих двух индексов. На самом деле индекс t в скрытом виде присутствует и в формуле NPV, однако, для упрощения ее отображения он не вводится в явном виде.
Столь громоздкий вид формуле (5) придает использование индексов q и t практически для всех параметров, а также соответствующее двойное суммирование, необходимое для свертки потоков в условиях использования этих двух индексов. На самом деле индекс t в скрытом виде присутствует и в формуле NPV, однако, для упрощения ее отображения он не вводится в явном виде.
Использованием в формуле (5) индексов q и t подчеркивается необходимость учета значений параметров не просто как каких-то абстрактных чисел в отрыве от экономических реалий, а наоборот — в конкретном экономическом контексте: с учетом не только времени, но и экономического пространства. Ведь любой квалифицированный специалист прекрасно понимает, что стоимость доллара сегодня и стоимость доллара через 10 лет — это далеко не одно и то же, точно так же, как стоимость доллара в латиноамериканских банках и стоимость доллара в швейцарских банках — разные величины. И вероятности, и риски, ассоциируемые с тем или иным денежным потоком, будут иметь не только временную, но и пространственную структуру. То есть важно учитывать не только, в какой момент времени возникнет тот или иной денежный поток, но и в какой точке экономического пространства он возникнет. Это может существенно повлиять на нашу оценку вероятностей и рисков, присущих каждому конкретному денежному потоку.
Если же необходимость столь точного измерения стоимости отсутствует, или же недостаточно исходной информации, то можно шаг за шагом упрощать формулу (5), что, к сожалению, будет приводить также к снижению уровня адекватности получаемых результатов.
Следует подчеркнуть, что использование понятия условно-денежных потоков (CCF — conventionally cash flows) вместо понятия денежных потоков (CF — cash flows) не случайно, а обусловлено необходимостью наиболее полного учета последствий экономических решений. В то время как термин «денежный поток» предполагает учет лишь денежных средств и их эквивалентов, термин «условно-денежный поток» подразумевает учет любых объектов экономических отношений, выраженных в денежном эквиваленте, и, следовательно, является более емким по содержанию [3].
При рассмотрении следующего примера (табл. 2) за основу взяты данные табл. 1. Осуществим ряд упрощающих допущений. Допустим, что вероятность (pXt) возникновения всех положительных условно-денежных потоков (Xt) одинакова и составляет 90%. Вероятность (PУt) возникновения всех отрицательных условно-денежных потоков (Yt) условно принимается равной 95%. Величина дополнительных отрицательных условно-денежных потоков (yt) для всех отрицательных условно-денежных потоков (Yt) принята равной 20% от величины последних. Вероятность (Pyt) возникновения дополнительных отрицательных условно-денежных потоков (yt) принята равной 30% для всех этих потоков. Годовая ставка дисконта принята равной 10% для всех условно-денежных потоков как положительных, так и отрицательных.
| 0 | 1 | 2 | 3 | 4 | 5 | |
| Безрисковая годовая ставка дисконта rt', % | 10 | 10 | 10 | 10 | 10 | |
| Положительные условно – денежные потоки (Xt), тыс. у.е. | 2900 | 4500 | 4200 | 1500 | 500 | |
| Вероятность возникновения положительных условно – денежных потоков (PXt) | 0,9 | 0,9 | 0,9 | 0,9 | 0,9 | |
| Положительные условно – денежные потоки с учетом вероятностей и рисков ( Xt * PXt), тыс. у.е. | 2610 | 4050 | 3780 | 1350 | 450 | |
| Экономические риски , связанные с положительными условно – денежными потоками ( Хt-Хt*PXt), тыс. у.е. | 290 | 450 | 420 | 150 | 50 | |
| Отрицательные условно – денежные потоки (Y,t), тыс. у.е. | 3000* | 1800 | 2300 | 2200 | 1900 | 1500 |
| Вероятность возникновения отрицательных условно – денежных потоков (PYt) | 1 | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 |
| Отрицательные условно – денежные потоки с учетом вероятностей ( Yt*PYt), тыс. у.е. | 3000 | 1710 | 2185 | 2090 | 1805 | 1425 |
| Дополнительные отрицательные условно – денежные потоки (yt) | 360 | 460 | 440 | 380 | 300 | |
| Вероятность возникновения дополнительных отрицательных условно – денежных потоков (pyt) | 0,3 | 0,3 | 0,3 | 0,3 | 0,3 | |
| Экономические риски , связанные с отрицательными условно – денежными потоками ( yt – Pyt, тыс. у.е. | 108 | 138 | 132 | 114 | 90 | |
| Отрицательные условно – денежные потоки с учетом вероятностей и рисков ( Уt*РYt + уt*Рyt), тыс. у.е. | 3000 | 1818 | 2323 | 2222 | 1919 | 1515 |
| Чистые условно – денежные потоки с учетом вероятностей и рисков ( Хt*PXt – Уt*PYt – yt*Pyt ), тыс. у.е. | -3000 | 792 | 1727 | 1558 | -569 | -1065 |
| Приведенная стоимость чистых условно – денежных потоков с учетом вероятностей и рисков (PVt), тыс. у.е. | -3000 | 720 | 1427 | 1171 | -389 | -661 |
| Чистая приведенная стоимость с учетом вероятностей и рисков , рассчитанная по «золотой формуле CCF » , тыс. у.е. | -732 |
Как видно из табл. 2, «золотая формула CCF» позволяет учесть не только вероятности, присущие конкретным положительным и отрицательным условно-денежным потокам, но и свойственные им экономические риски. Так, например, в строке «Экономические риски, связанные с положительными условно-денежными потоками» зафиксированы суммы, на которые соответствующие положительные условно-денежные потоки могут оказаться меньше прогнозируемых. А в строке «Экономические риски, связанные с отрицательными условно-денежными потоками» зафиксированы суммы, на которые соответствующие отрицательные условно-денежные потоки могут превысить запланированные.
В результате использования более корректного подхода к учету вероятностей и экономических рисков, предусмотренного «золотой формулой CCF», в рассматриваемом примере величина чистой приведенной стоимости оказывается отрицательной ( – 732 тыс. у.е.).
Вместе с тем, следует особо подчеркнуть, что стоимость, рассчитываемая по «золотой формуле CCF» в конкретных ситуациях может оказываться как ниже, так и выше стоимости, рассчитываемой по традиционным формулам NPV. Поэтому было бы ошибочно полагать, что «золотая формула CCF» во всех случаях дает более пессимистичные или более оптимистичные результаты, по сравнению с результатами формул метода NPV.
Таким образом, «золотая формула CCF» позволяет эффективно решать проблему неадекватности учета вероятностей и экономических рисков, связанных с денежными потоками, присущую методу NPV и методу реальных опционов.
В заключение хотелось бы отметить, что хотя создание «золотой формулы CCF» существенно усовершенствовало механизм измерения стоимости в условиях неопределенности, мы не остановились на этом в наших исследованиях. Их продолжение позволило нам существенно усовершенствовать «золотую формулу CCF», заменив в ней традиционную концепцию дисконтирования на субъектно-ориентированную концепцию Галасюка, учитывающую экономические риски, связанные с существованием не объекта экономических отношений, а субъекта экономических отношений. Полученный результат получил название «платиновая формула CCF»:
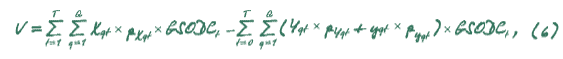
Ключевым отличием «платиновой формулы CCF» от «золотой формулы CCF» является использование вместо «традиционного» коэффициента дисконтирования субъект -но-ориентированного коэффициента дисконтирования Галасюка (GSODС — Galasyuks' subject oriented discounting coefficient). Использование «платиновой формулы CCF» вместо «золотой формулы CCF» или вместо формулы NPVприводит к существенным практическим последствиям. Подробно осветить практику применения «платиновой формулы CCF» мы надеемся в наших последующих работах. Именно «платиновая формула CCF», сегодня является наиболее адекватным методом определения стоимости в условиях неопределенности, поскольку она обеспечивает возможность корректного учета вероятностей и экономических рисков, присущих как объектам экономических отношений, так и субъектам этих отношений. Кроме того, «платиновая формула CCF» может быть использована для усовершенствования метода реальных опционов.
Таким образом, учет принципа субъективной асимметричности экономических оценок в «золотой» и «платиновой» формулах CCF позволяет решить фундаментальную проблему некорректности учета экономических рисков в методе NPVи методе реальных опционов.

