Достоинства и недостатки методов оценки инвестиционных проектов

Достоинства и недостатки методов оценки инвестиционных проектов

Если вы собственник или топ-менеджер организации, то вам, вероятно, постоянно приходится принимать решения, связанные с инвестированием средств в тот или иной бизнес, в расширение существующего производства либо замену устаревшего оборудования.

Чем вы обычно руководствуетесь при принятии таких решений? Безусловно, перспектива освоить новый бизнес всегда заманчива, инвестиционные проекты могут иметь политические и благотворительные цели, но наверняка главным критерием для вас является экономическая эффективность инвестиционного проекта. Основная сложность заключается в том, что всегда есть возможность альтернативного вложения (в том числе в финансовые институты), и выбор «принять/отклонить» сводится к решению «выбрать оптимальный проект». Но для принятия эффективного решения необходима информация, в первую очередь – информация о доходности инвест-проекта.

Как подсчитать эффективность?

Наиболее простой способ оценки инвест-проекта – рассчитать бухгалтерскую прибыль, среднегодовую рентабельность и период окупаемости (количество лет, за которое окупаются первоначальные инвестиции). Но даст ли нам это информацию, необходимую для принятия решений? Ответ однозначен – нет, не даст. Дело в том, что эти методы не учитывают того обстоятельства, что деньги лучше получить раньше, чем позже. Это наглядно показано на простом примере (табл. 1).

Таблица 1

Год	2004	2005	2006	2007	Прибыль
Проект А	-100 тыс.	100 тыс.	90 тыс.	5 тыс.	95 тыс.
Проект В	-100 тыс.	100 тыс.	5 тыс.	100 тыс.	105 тыс.

Выбор оптимального проекта на основе величины бухгалтерской прибыли (здесь и далее в таблицах показатели приведены в условных денежных единицах) Бухгалтерские методы вам покажут, что проект Б является более эффективным, но, возможно, все же лучше выбрать проект А?

Концепция стоимости денег во времени

Прежде всего необходимо сказать, что при оценке инвест-проектов мы оцениваем деньги. Инвест-проект требует денежных вложений и генерирует денежные потоки. Более того, мы оцениваем чистые денежные потоки за период, то есть поступления минус расходы.

Деньги сегодня стоят дороже, чем деньги завтра. Этот принцип лежит в основе всех финансовых расчетов. Почему?

Ну, во-первых, потому что имея сегодня 1 доллар, вы через год получите 1 доллар 10 центов, не прилагая никаких усилий, а просто положив деньги в банк практически без риска. Первый важный вывод состоит в том, что деньги стоят дороже сегодня, потому что существует возможность их безрискового вложения.

Во-вторых, деньги сегодня стоят дороже, потому что существует неопределенность их получения в будущем. Поэтому, выбирая между проектами, необходимо учитывать степень риска каждого из них. Следовательно, нам нужен метод, который позволит сравнивать денежные потоки, получаемые в различные периоды времени (например, годы) с различным уровнем риска.

Методы дисконтированной стоимости

Основной принцип сравнения денежных потоков заключается в расчете того, сколько сегодня стоят «будущие» деньги, то есть необходимо из денежных потоков исключить безрисковую ставку процента и компенсацию рисков.

Операция расчета «сегодняшней» стоимости «будущих» денег называется дисконтированием. Ставка процента, с помощью которой «будущие» денежные средства приводятся к настоящему моменту, называется ставкой дисконтирования.

Как определить эту ставку?

1. Безрисковую часть рассчитать достаточно просто – она равна ставке безрисковых вложений. (Например, ставка по облигациям госзайма в США является безрисковой ставкой. В Украине определить безрисковую ставку сложнее, так как даже государственному займу присуща определенная степень риска, но ставку процента по госзайму можно рассматривать в качестве ориентира.)

2. Компенсацию за риск могут оценить банковские специалисты, просто необходимо отнести ваш бизнес-план в банк: та ставка, по которой вам предложат кредит, может быть близка к реальности. Но это не обязательно так, ведь в банке оценивают не только риск неудачи проекта, но и финансовую устойчивость и способность самой компании погасить кредит.

3. За ставку дисконтирования можно принять ставку доходности на фондовом рынке по ценным бумагам с таким же уровнем риска, как и у проекта. Конечный выбор ставки дисконтирования будет определяться предпочтениями и ожиданиями инвестора.

Метод чистой дисконтированной стоимости – NPV (Net Present Value) NPV является прибылью от проекта за вычетом цены денег и доплаты за риск.

Рассчитав NPV для рассмотренного ниже примера (табл. 2), мы можем выбирать между проектами А и Б. Допустим, безрисковая ставка равна 10%, а компенсация рисков по обоим проектам составляет 10% (но мы можем сравнивать проекты и с разным уровнем риска). Значит, ставка дисконтирования равна 20%.

Таблица 2.
Выбор оптимального проекта на основе NPV

Год	2004	2005	2006	2007	NVP
Проект А	-100 тыс.	100 тыс.	90 тыс.	5 тыс.
Стоимость «будущих денег» в 2003 г.	-83,3 тыс.	69,4 тыс.	52 тыс.	2,4 тыс.	40,6 тыс.
Проект В	-100 тыс.	100 тыс.	5 тыс.	100 тыс.
Стоимость «будущих денег» в 2003 г.	-83,3 тыс.	69,4 тыс.	2,8 тыс.	48,2 тыс.	37,2 тыс.

Таким образом, мы видим, что с точки зрения стоимости денег во времени предпочтительнее проект А, хотя бухгалтерская прибыль по этому проекту меньше. Общее правило выбора проекта (из нескольких) состоит в том, что выбирается проект с наибольшим NPV. Естественно, для того чтобы проект был выбран, показатель NPV должен быть положительным (зачем реализовывать убыточные проекты?).

Недостаток данного метода в том, что он показывает абсолютную величину прибыли. Сделав вклад в банк в размере 1000 долларов под 15% годовых, через год вы получите больше прибыли, чем если бы вы сделали вклад в размере 500 долларов (под те же 15%). Иными словами, для проектов с различным уровнем инвестиций метод NPV не подходит.

Следовательно, для оптимального выбора нам необходим показатель, который дает оценку доходности проекта и аналогичен по смыслу бухгалтерской рентабельности, но при этом учитывает стоимость денег во времени.

Метод внутренней нормы доходности – IRR (Internal Rate Of Return)
IRR является доходностью проекта.

Формула показывает способ расчета внутренней нормы доходности (математически IRR – это сложная средневзвешенная величина).

Таблица 3
Выбор оптимального проекта на основе IRR

Год	2004	2005	2006	2007	NVP	IRR
Проект А	-100 тыс.	100 тыс.	90 тыс.	5 тыс.	40,6 тыс.	59%
Проект В	-100 тыс.	100 тыс.	5 тыс.	100 тыс.	37,2 тыс.	46%

Рассчитав IRR для проектов А и Б из нашего примера, мы выберем проект А. Заметим, что в данном случае оба метода (NPV и IRR) показывают одинаковый результат (проект А предпочтительнее), что бывает далеко не всегда.

Общее правило состоит в том, что проект принимается к реализации, если у него IRR выше безрисковой ставки доходности и компенсации рисков. Среди нескольких проектов выбирается тот, у которого больший IRR.

Ставка реинвестирования

Вспомним концепцию стоимости денег во времени: деньги имеют стоимость потому, что существует возможность их альтернативного вложения. Поэтому методы дисконтированной стоимости (NPV и IRR) предполагают, что существует возможность реинвестирования либо по ставке дисконтирования, либо по IRR. Это означает, что деньги, полученные в любой период времени, можно дополнительно разместить (и получить доход) по ставке реинвестирования.

Это очень важное условие. Оно ограничивает выбор ставки дисконтирования условием, что она должна не только отражать ожидания инвестора относительно проекта, но и обязательно соответствовать рыночным ставкам доходности. То есть для сравнения денег в 2003 и 2004 годах необходимо выбрать такую ставку дисконтирования, чтобы на фондовом рынке существовал финансовый инструмент с сопоставимой доходностью (с соответственным уровнем риска).

Сравнительный анализ методов NPV и IRR

Всегда ли методы NPV и IRR приводят нас к оптимальному решению? Увы, бывают случаи, когда результаты вводят инвестора в заблуждение. Рассмотрим достоинства и недостатки методов с помощью табл. 4.

Таблица 4
Сравнение методов NPV и IRR

Метод	Достоинства	Недостатки
NPV	1. Имеет понятное экономическое определение 2. Учитывает стоимость денег во времени 3. Ставка реинвестирования, как правило, не высока, и расчет не приводит к большим ошибкам 4. Позволяет учесть то обстоятельство, что ставки дисконтирования со временем меняются	1. NVP – абсолютный показатель, поэтому метод не позволяет сделать выбор между проектами с разным объемом инвестиций.
IRR	1. Является относительным показателем 2. Сопоставим с доходностью ценных бумаг и банковским процентом 3. Учитывает стоимость денег во времени 4. Не зависит от ставки дисконтирования	1. Формула расчета IRR не имеет понятного определения 2. IRR показывает одинаковое значение в том случае, когда мы берем в кредит и когда даем взаймы 3. У проекта может существовать несколько значений IRR (при этом все значения могут быть неадекватны) или их может не быть вовсе. Эта особенность связана с математическим методом расчета IRR 4. NVP и IRR могут показывать противоположные результаты вовзаимоисключающих проектах даже при одинаковых объемах инвестиций. 5. Не позволяет учесть изменение во времени ставок дисконтирования 6. Посколько IRR является ставкой реинвестирования, то при высокой величине IRR небольшое изменение во временной структуре денежных потоков приводит к значительному изменению IRR

Поскольку о недостатках NPV мы уже говорили ранее, рассмотрим подробно недостатки IRR.

1. Формула расчета IRR не имеет понятного определения.
Финансовый менеджер постоянно сталкивается с необходимостью объяснять инвестору, что же такое IRR. Математически IRR определяется как ставка дисконтирования, при которой NPV равна нулю. Но, к сожалению, не существует понятного экономического определения, которое можно увязать с математической формулой.

2. IRR показывает одинаковое значение в том случае, когда мы берем кредит и когда даем взаймы. Рассмотрим это на примере (см. табл. 5):
Внутренняя норма доходности одинакова, но это не означает, что проекты одинаково привлекательны. Данная проблема приводит к третьему недостатку.

Таблица 5
«Ловушка» кредитования

Год	2004	2005	IRR	NVP
Проект 1	-1000	1500	50%	364
1000	-1500	50%	-364

3. У проекта может существовать несколько значений IRR (при этом все значения могут быть неадекватны) или их может не быть вовсе.

Если проект в процессе реализации требует дополнительных инвестиций и денежные потоки становятся отрицательными (меняют знак), то будет существовать несколько значений IRR либо их вообще не будет. Кроме того, найденные значения могут быть неадекватны. Рассмотрим на примере (см. табл. 6).

Таблица 6
Множественные значения IRR

Год	2004	2005	2006	IRR	NVP при r=10%
Проект 1	-4000	25000	-25000	25% и 400%	-1934

В этой ситуации оба значения IRR могут привести к ошибочным выводам (оба неадекватны). В данном случае NPV растет с ростом ставки дисконта.

4. NPV и IRR могут показывать противоположные результаты во взаимоисключающих проектах при одинаковых объемах инвестиций.

Рассмотрим этот случай на примере (см. табл. 7). Сравнивая два варианта (допустим, продажу объекта недвижимости и сдачу его в аренду), мы видим, что NPV значительно выше у проекта 2, но IRR выше у проекта 1. Почему так происходит? Ответ виден на графике 1. На нем показана зависимость NPV от ставки дисконтирования. При росте ставки дисконтирования NPV обоих проектов снижается. До точки пересечения методы показывают противоположные результаты, точка пересечения линий с осью Х дает нам ставки IRR. Экономически это объясняется тем, что когда цена денег невысока, бессрочная рента является предпочтительнее, а когда цена капитала значительна, то выгоднее продажа объекта. В ситуации с взаимоисключающими проектами лучшим критерием для выбора является NPV (при одинаковом уровне инвестиций).

График 1. Ставка дисконтирования и NPV.

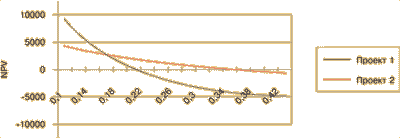
Ставка дисконтирования

Таблица 7
Противоречие методов NPV и IRR

Год	2004	2005	2006	2007	2008	2..	IRR	NVP при r=10%
Проект 1	-9000	6000	5000	4000			33%	3592
Проект 2	-9000	1800	1800	1800	1800	и т.д.	20%	9000

5. Не позволяет учесть изменение во времени ставок дисконтирования.
Оба метода предполагают, что ставки дисконтирования постоянны во времени, то есть безрисковая ставка доходности и сумма компенсации рисков не изменяются на протяжении всего проекта (IRR является ставкой дисконтирования). На самом деле это не так – ставки процента меняются из года в год. Метод NPV позволяет учесть этот факт (как показано в математическом приложении 4, помещенном на CD-приложении), а вот метод IRR – нет.

6. Поскольку IRR является ставкой реинвестирования, то при высокой величине IRR небольшое изменение во временной структуре денежных потоков приводит к значительному изменению IRR. Представьте, что вам необходимо принять решение по строительному проекту. В 2004 году вы покупаете стройплощадку за 1000 дол. Стоимость строительства равна 10000 дол., срок строительства составляет 2 года, в течение которых происходят равномерные расход стройматериалов и выплата заработной платы. В конце строительства вы получаете 3000 дол. прибыли.

Выбирая заказчика под проект, вы можете предложить два условия предоплаты: полностью в первый год, либо по 5000 дол. ежегодно. Рассчитывая IRR (табл. 8), вы видите, что в варианте 100%-ной предоплаты он почти в 7 раз больше! Но отражает ли это экономическую предпочтительность этого варианта? Стоит ли торговаться с заказчиком ради семикратного увеличения IRR, рискуя потерять заказчика? Ответ – не стоит. Метод предполагает, что получаемые средства в любой год можно реинвестировать (вложить и получить доходность) по ставке IRR. Реинвестировать деньги под 292% на год – невозможно. Данная ситуация демонстрирует случаи, когда IRR неадекватен. Здесь поможет показатель MIRR (см. ниже).

Таблица 8
Результат реинвестирования по IRR

Год	2004	2005	2006	2007	NVP при r=15%	IRR
Проект 1	-1000	0	0	3000	845,69	44%
Проект 2	-1000	5000	-5000	3000	1 338,83	292%

Стоит ли отказываться от IRR?

Часто ли встречаются ситуации, подобные описанным в этом разделе? Нет, не часто, но определенная вероятность их возникновения существует. Зачастую вы можете пользоваться этими показателями, не зная об их недостатках. К тому же, несмотря на все недостатки данного метода, он единственный показывает внутреннюю доходность проекта, не зависимую от ставки дисконтирования и сопоставимую с финансовыми инструментами. Поэтому мы предлагаем вместо вопроса: «Чем заменить IRR?» поставить вопрос: «Как проверить корректность IRR?»

Метод модифицированной внутренней нормы доходности – MIRR (Modified Internal Rate Of Return) В математическом приложении 5, помещенном на СD-приложении, описано, как рассчитывается данный показатель, который лишен недостатков IRR. Но мы предлагаем рассматривать его не как отдельный показатель, а как метод проверки корректности IRR для данного проекта. Например, если существует несколько значений IRR, сопоставление их с MIRR позволит отбросить неадекватные значения. Фактически MIRR по методике расчета ближе к NPV, потому что зависит от ставки дисконтирования. А ведь доходность проекта не долж-на зависеть от изменений рыночных ставок процента!

5 рекомендаций, как оценить инвест-проекты, избежав ошибок

1. Определите, являются ли проекты взаимоисключающими (например, разные варианты использования одной стройплощадки). Узнайте, возможно ли повторить проект в будущем.

Условия	Проект возможно повторить несколько раз	Проект невозможно повторить
Проекты взаимоисключающие	NVP, IRR (MIRR)	IRR (MIRR)
Проекты не взаимоисключающие	NVP	IRR (MIRR), NVP

2. Если проекты имеют различный уровень инвестиций, вам необходим IRR (MIRR).

3. Сравнивая значения IRR и MIRR, определяйте адекватность IRR. Если IRR неадекватен, используйте MIRR.

4. Постройте график зависимости NPV от ставки дисконтирования и определите, при какой ставке дисконтирования NPV и IRR показывают противоречивые результаты. Проанализируйте возможность возникновения такой ситуации.

5. Уделите особое внимание показателю IRR в случае, если он имеет большую величину, значительно (на порядок) отличающуюся от рыночной ставки дисконтирования. Определите возможность реинвестирования по ставке IRR.

Заключение

Объяснить всю работу по выбору критериев оценки бизнес-проектов, не вдаваясь в технические подробности, чрезвычайно сложно. Некоторые недостатки методов имеют чисто математическую основу. Здесь важно понять, что не все методы можно применять во всех ситуациях. Окончательные рекомендации по выбору критериев оценки и проведению расчетов лучше доверить специалисту по инвестиционному менеджменту. Он поможет вам, избежав ошибок, оценить доходность и риски, однако окажется ли решение принять их на себя правильным, во многом зависит от вашей предпринимательской интуиции. Во всяком случае, количественно оценивая эффективность, вы будете ясно представлять:

1. Чем вы рискуете.

2. Что вы можете получить в случае успеха.

Уверяем вас, что, располагая такой информацией, вы значительно повысите точность ваших решений