Впервые мы столкнулись с проблемами планирования капитальных вложений в главе 2. Там мы практически не касались решений по финансированию, приняв за исходную предпосылку простейший случай — а именно финансирование полностью из собственного капитала. По сути, там мы представили идеальный мир Модильяни—Миллера (ММ), в котором никакие решения по финансированию не имеют значения. В строгой модели ММ фирмы могут анализировать реальные инвестиции так, словно бы единственным источником их финансирования являлся собственный капитал, а реальный финансовый план — это не более чем пустяковая деталь, которую можно оставить на потом.
Согласно допущениям ММ, решения о том, как тратить деньги, отделены от решений о том, как их добывать. В этой главе мы снова обратимся к бюджетному планированию, но уже при условии, что инвестиционные решения и решения по финансированию взаимосвязаны, и их нельзя полностью отграничить друг от друга.
Из предыдущих глав вы узнали, как оценивать инвестиционные возможности в четыре действия:
- составить прогноз посленалогового денежного потока при условии, что проект финансируется полностью из собственного капитала;
- оценить риск, присущий проекту;
- оценить альтернативные издержки привлечения капитала, то есть ожидаемую доходность, которую обеспечивают инвесторам обращающиеся на рынке капитала инвестиционные инструменты с эквивалентным риском;
- исчислить чистую приведенную стоимость по формуле дисконтированного денежного потока.
По сути, до сих пор мы рассматривали всякий проект как мини-фирму и задавались вопросом: «Сколько стоила бы эта мини-фирма, если бы мы вычленили ее в самостоятельное предприятие, финансируемое только из собственного капитала? Сколько инвесторы согласились бы заплатить за его акции (т. е. за участие в проекте)?».
Разумеется, в основе этой методики лежит принцип слагаемости стоимостей. На хорошо работающих рынках капитала рыночная стоимость фирмы представляет собой сумму приведенных стоимостей всех имеющихся у фирмы активов — то есть целое равно сумме всех его составных частей.
В этой главе мы по-прежнему придерживаемся принципа слагаемости стоимостей, но в более широком смысле — распространив его на стоимость, обусловленную решениями по финансированию. Это можно сделать двумя способами.
- Коррекция ставки дисконтирования, обычно это поправка в сторону понижения сообразно включению в расчет процентной налоговой защиты. Это самый распространенный прием. Как правило, поправка производится введением посленалоговых средневзвешенных затрат на капитал (WACC).
- Коррекция приведенной стоимости, когда сначала оценивается базовая стоимость проекта как самостоятельной мини-фирмы, финансируемой полностью из собственного капитала, а затем в эту базовую NPV вносятся поправки, отражающие влияние проекта на структуру капитала компании:
Скорректированная NPV (APV) = базовая NPV + NPVрешения по финанированию проекта
Как только вы выявили и оценили побочные эффекты финансирования проекта, исчисление его скорректированной чистой приведенной стоимости (для краткости APV) сводится к элементарным арифметическим действиям.
Эта глава представляет собой практикум стоимостной оценки с учетом финансирования. В первом разделе мы объясним, в чем смысл понятия после-налоговых средневзвешенных затрат на капитал и как выводится этот показатель. Здесь же вы познакомитесь с необходимыми предпосылками и типичными ошибками, совершаемыми при использовании формулы WACC. Затем в разделе 19.2 мы проведем «уроки мастерства»: опишем специфические приемы, которые облегчают оценку вводимых параметров формулы и ее практическое применение. Раздел 19.3 покажет, как пересчитывать WACC при изменении структуры капитала или набора активов фирмы.
В разделе 19.4 мы займемся методом APV. В самом методе нет ничего особенно сложного: вы просто оцениваете проект дисконтированием по альтернативным издержкам привлечения капитала (но не по WACCI), а затем прибавляете к этой оценке прирост или потерю приведенной стоимости, вызванные побочными эффектами решений по финансированию. Но вот выявление и оценка самих этих побочных эффектов порой требуют изрядной сноровки, поэтому тут нам придется проработать несколько числовых примеров.
В разделе 19.5 мы вернемся к основному и, казалось бы, простому вопросу: какой должна быть ставка дисконтирования для безрисковых проектов? Если принять во внимание тот факт, что проценты по долгу подлежат вычету из налоговой базы, то сразу становится ясно: стоимость всех безрисковых, или эквивалентных долгу, денежных потоков можно оценивать дисконтированием по посленалоговои процентной ставке. Как мы увидим, это правило остается в силе и для WACC, и для APV.
Заключительный раздел главы посвящен ответам на некоторые замысловатые вопросы, которые зачастую ставят в тупик менеджеров и студентов. На веб-сайте Брейли—Майерса вы можете найти своего рода приложение к этой главе, где излагаются дополнительные сведения и формулы по теме2.
ПОСЛЕНАЛОГОВЫЕ СРЕДНЕВЗВЕШЕННЫЕ ЗАТРАТЫ НА КАПИТАЛ
Давайте мысленно вернемся к главе 17 и Первому постулату Модильяни—Миллера (ММ). Как показывают ММ, в отсутствие налогов и других несовершенств финансового рынка величина затрат на капитал не зависит от способа финансирования. Иначе говоря, средневзвешенная ожидаемых доходностей долга и акций для инвесторов равна альтернативным издержкам привлечения капитала вне зависимости от коэффициента долговой нагрузки:
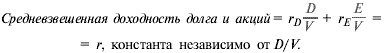
Здесь г— это альтернативные издержки привлечения капитала, или доходность, которую требовали бы инвесторы, если бы фирма совсем не имела долга; гд и г^ — ожидаемые доходности акций и долга, то есть «затраты на заемный капитал» и «затраты на собственный капитал»; весовые коэффициенты D/Vn E/V— доли долга и собственного капитала в рыночной стоимости; V— совокупная рыночная стоимость фирмы, сумма D иЕ.
Но вы не найдете значений г (альтернативных издержек привлечения капитала) ни в деловой прессе, ни в Интернете. Поэтому финансовые менеджеры подходят к проблеме с другого бока: сперва определяют гд и г^, а уж из них выводят значение г. В модели ММ:

Согласно этой формуле, альтернативные издержки привлечения капитала, г, определяются как ожидаемая доходность портфеля всех обращающихся ценных бумаг фирмы. Мы уже разбирали эту формулу средневзвешенных затрат на капитал в главах 9 и 17. Но она не отражает коренного различия между долгом и собственным капиталом (акциями): процентные платежи по долгу подлежат вычету из налоговой базы. Поэтому мы переходим к посленалоговым средневзвешенным затратам на капитал, которые принято обозначать WACC.
WACC= rD(\-Tc)y+rEy,
где Тс — предельная ставка корпоративного налога.
Обратите внимание, что посленалоговые средневзвешенные затраты на капитал (WACC) меньше альтернативных издержек (г), поскольку «затраты на заемный капитал» рассчитываются в посленалоговом выражении как rD(\ — Тс). Таким образом, налоговое преимущество долгового финансирования проявляется в более низкой ставке дисконтирования. Заметьте также, что все переменные в формуле средневзвешенных затрат на капитал относятся к фирме в целом. Следовательно, формула дает нам верную ставку дисконтирования только для проектов, которые по всем характеристикам схожи с осуществляющей их фирмой. Формула хороша для «среднего» проекта. Но она не годится для проектов, которые отличаются большей надежностью или, наоборот, более высоким риском, нежели в среднем активы фирмы. И, значит, она не годится для проектов, осуществление которых ведет к увеличению или уменьшению коэффициента долговой нагрузки фирмы.
Пример: корпорация «Полная чаша»
Давайте вычислим WACC для корпорации «Полная чаша», чьи балансы в бухгалтерских и рыночных показателях выглядят следующим образом (в млн дол.):
| Балансовая стоимость | |
| Стоимость активов 100 100 |
50 Долг 50 Собственный капитал 100 |
| Рыночная стоимость | |
| Стоимость активов 125 125 |
50 Долг (D 75 Собственный капитал (Е) 125 Стоимость фирмы (V) |
Мы подсчитали рыночную стоимость собственного капитала «Полной чаши» умножением текущей цены ее акций (7,50 дол. за акцию) на число акций в обращении (10 млн). Компания процветает и имеет хорошие перспективы, так что ее акции продаются дороже балансовой стоимости (5,00 дол. за акцию). Однако значения балансовой и рыночной стоимости долга в этом примере равны.
Затраты компании на заемный капитал (процентная ставка по нынешнему долгу и любым будущим долгам) составляет 8%. Ее затраты на собственный капитал (ожидаемая доходность, требуемая инвесторами в акции) — 14,6%.
Баланс «Полной чаши» по рыночной оценке показывает активы стоимостью 125 млн дол. Разумеется, мы не можем наблюдать эту стоимость напрямую, ведь сами по себе активы не продаются. Но мы знаем, чего они стоят инвесторам в долговые обязательства и акции компании (50 млн + 75 млн = 125 млн дол.). Эта сумма отражена в левой части баланса, составленного по рыночной оценке.
А зачем нам понадобился баланс в бухгалтерских показателях? Лишь затем, чтобы поставить на нем жирный крест. Что вы и можете исполнить немедленно.
При оценке средневзвешенных затрат на капитал нас не интересуют прошлые инвестиции — только текущие значения стоимости и ожидания на будущее. Подлинный коэффициент долговой нагрузки компании равен вовсе не 50% (как следует из бухгалтерских показателей), а 40%, ибо ее активы реально стоят 125 млн дол. Затраты на собственный капитал (гЕ = 0,146) — это ожидаемая инвесторами доходность от покупки акций по текущей рыночной цене 7,50 дол. за акцию, а не по номинальной (балансовой) стоимости: ведь вы уже не сможете купить акции «Полной чаши» по 5 дол.
«Полная чаша» — устойчиво прибыльная компания и платит налог по предельной ставке 35%. Это последняя недостающая переменная для формулы WACC. Вот сводка всех вводимых параметров формулы:
- Затраты на заемный капитал rD = 0,08
- Затраты на собственный капитал лЕ = 0,146
- Предельная ставка налога 7с = 0,35
- Коэффициент долговой нагрузки D/V= 50/125 = 0,4
- Коэффициент собственного капитала E/V= 75/125 = 0,6
Итак, посленалоговые средневзвешенные затраты компании на капитал равны:
WACC= 0,08 х (1 – 0,35) х 0,4 + 0,146 х 0,6 = 0,1084, или 10,84%.
Ну вот вы и вычислили
Теперь давайте посмотрим, как «Полная чаша» должна распорядиться этой формулой. Виноделы компании планируют инвестировать 12,5 млн дол. в создание вечного двигателя для виноградодавильни, то есть машины, которая — на редкость удачно для наших расчетов! — никогда не изнашивается и производит постоянный денежный поток по 2,085 млн дол. в год (в доналоговом выражении). Тогда посленалоговый денежный поток составит (в млн дол.):
- Доналоговый денежный поток 2,085
- Налог по ставке 35% 0.730
- Посленалоговый денежный поток 1,355
Заметьте: посленалоговый денежный поток никак не отражает налоговую защиту по долгу, связанному с проектом вечного двигателя. Как мы уже объясняли в главе 6, в обычной практике бюджетного планирования посленалоговый денежный поток исчисляется так, словно бы проект финансировался целиком из собственного капитала. Однако это не означает, что процентная налоговая защита не будет учтена вовсе: мы собираемся дисконтировать денежный поток от этого проекта «Полной чаши» по ее WACC, куда затраты на заемный капитал включены уже в посленалоговом выражении. Стоимость налоговой защиты проявляется не в большей величине посленалогового денежного потока, а в сниженной ставке дисконтирования.
Коль скоро вечный двигатель производит постоянный по величине денежный поток С = 1,355 млн дол., чистая приведенная стоимость равна:
NPV = – $ 12 500 000 + $ 1 355 000 / 0.1084 = 0
Нулевая NPV означает, что планируемые капиталовложения балансируют на грани допустимого. Годовой денежный поток в размере 1,355 млн дол. оборачивается доходностью инвестиций 10,84% (1,355/12,5= 0,1084), что в точности равно WAСС компании. Когда NPV= 0, доходность для инвесторов в акции должна полностью уравниваться с затратами компании на собственный капитал (14,6%). Давайте удостоверимся в том, что акционеры «Полной чаши» действительно могут ожидать такой доходности от своих инвестиций в проект вечного двигателя.
Допустим, «Полная чаша» рассматривает проект как отдельную мини-фирму. Ее баланс в рыночных ценах выглядел бы следующим образом (в млн дол.):
| ВЕЧНЫЙ ДВИГАТЕЛЬ | |
| Рыночная стоимость | |
| Стоимость проекта 12,5 12,5 |
5,0 Долг (D) 7.5 Собственный капитал (Е) 12,5 Стоимость проекта (V) |
Рассчитаем ожидаемый денежный доход акционеров (в млн дол.):
Посленалоговые проценты = rD(\ – TC)D= 0,08 х (1 – 0,35) х 5 = 0,26
Ожидаемый доход по акциям = С— (1 — Tl)rDD= 1,355 — 0,26 = 1,095.
Проект приносит постоянную и бессрочную прибыль, поэтому ожидаемая доходность акций должна быть равна ожидаемому денежному доходу по акциям, деленному на стоимость акций:
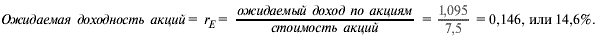
Ожидаемая доходность акций равна затратам компании на собственный капитал, и это объясняет, почему чистая приведенная стоимость проекта равна нулю.
Обзор предпосылок
Дисконтируя постоянный денежный поток от проекта по WACC компании, мы исхо-дим из следующих предпосылок:
- проект сопряжен с таким же деловым риском, как и остальные активы компании;
- для проекта характерно такое же отношение долга к стоимости, какое заложено в структуре капитала компании в целом.
Из нашего примера легко увидеть, насколько важны эти две предпосылки: если проект вечного двигателя будет отличаться более высоким риском, нежели остальные активы «Полной чаши», или если осуществление проекта повлечет за собой устойчивые существенные4 изменения коэффициента долговой нагрузки компании, то ее акционеры не удовлетворятся 14,6% ожидаемой доходности от своих инвестиций в проект и затраты на собственный капитал возрастут.
Наша иллюстрация применения формулы WACC относится только к проекту, обеспечивающему постоянный денежный поток. Но Майлз и Иззель показали, что формула работает при любых схемах денежного потока, если только компания корректирует свою политику заимствования так, чтобы коэффициент долговой нагрузки со временем не менялся. Если же фирма отходит от такой политики заимствования, формула WACC дает лишь очень приблизительный результат.
ПРИМЕНЕНИЕ WACC: НЕСКОЛЬКО ПОЛЕЗНЫХ ПРИЕМОВ
«Полная чаша» располагает только одним активом и двумя источниками финансирования. У любой реальной компании содержание баланса гораздо разнообразнее, например:
| Оборотные активы , | Текущие обязательства , |
| включая денежные средства , | включая кредиторскую задолженность |
| товарно – материальные запасы , | и краткосрочный долг |
| дебиторскую задолженность | |
| Основные средства | Долгосрочный долг (D) |
| Привилегированные акции ( Р ) | |
| Перспективы роста | Обыкновенные акции ( Е ) |
| Стоимость сЬиомы (V) |
В связи с этим сразу же возникают несколько занимательных вопросов.
1. Как меняется формула при наличии более чем двух источников финансирования? Здесь все просто: у каждого элемента свои издержки. Весовым коэффициентом каждого элемента служит его доля в рыночной стоимости. Скажем, если в структуре капитала помимо долга представлены как привилегированные, так и обыкновенные акции, то: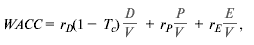
где Гр— доходность, ожидаемая инвесторами от привилегированных акций.
2. Как быть с краткосрочным долгом? Многие компании при расчете WACC принимают
во внимание только долгосрочные источники финансирования, пренебрегая издерж
ками краткосрочного заимствования. В принципе это неправильно. Кредиторы, вла – деющие краткосрочными долговыми обязательствами, — такие же инвесторы, как и
все остальные, и вправе претендовать на свою долю операционной прибыли. Компа – нии, которые не берут в расчет подобные претензии, рискуют неверно оценить тре
буемую доходность инвестиций.
Впрочем, «обнуление» краткосрочного долга — это не слишком серьезная ошибка, если такой долг носит временный, сезонный или случайный характер либо если он компенсируется наличием у компании достаточных денежных средств и легкореализуемых ценных бумаг7. Представьте себе, к примеру, что итальянский филиал вашей фирмы взял у итальянского банка шестимесячный кредит для финансирования своих товарно-материальных запасов и дебиторской задолженности. Денежный эквивалент этого займа получит отражение в балансе материнской компании как краткосрочный долг. В то же время материнская компания сама может предоставить кредит, вложив избыточную наличность в краткосрочные долговые ценные бумаги. Если суммы выданного и взятого кредитов уравновешиваются, нет смысла включать издержки краткосрочного заимствования в формулу средневзвешенных затрат на капитал, поскольку у компании нет чистой краткосрочной задолженности.
3.Как быть с прочими текущими обязательствами! Текущие обязательства обьгано «списывают со счетов», вычитая из оборотных активов. Разность получает отражение в левой части баланса как чистый оборотный капитал. Сумму долгосрочных источников финансирования в правой части баланса называют общей капитализацией.
| Чистый оборотный капитал = | |
| = оборотные активы – | |
| – текущие обязательства | Долгосрочный долг (D) |
| Основные средства | Привилегированные акции ( Р ) |
| Перспективы роста | Собственный капитал ( Е ) |
| Общая капитализация (V) |
Коль скоро чистый оборотный капитал отнесен к активам, при прогнозировании денежного потока для инвестиционного проекта любое увеличение чистого оборотного капитала следует рассматривать как отток, а любое уменьшение — как приток денежных средств. Это стандартная практика, с которой мы познакомились еще в разделе 6.2.
Краткосрочный долг входит в состав текущих обязательств, поэтому их вычитание из оборотных активов выводит издержки краткосрочного заимствования из расчета средневзвешенных затрат на капитал. Мы только что объяснили, в каких случаях и почему такое допущение вполне приемлемо. Но когда краткосрочный долг является важным и постоянным источником финансирования — что типично для малых фирм и для компаний за пределами США, — его следует неукоснительно показывать в правой части баланса, не вычитая из оборотных активов. Естественно, процентные платежи по краткосрочному долгу становятся при этом одним из элементов формулы средневзвешенных затрат на капитал.
4. Как исчислять затраты по отдельным элементам финансирования? Для оценки гЕ, ожидаемой доходности, требуемой инвесторами в акции компании, вы зачастую можете воспользоваться доступными данными фондового рынка. При наличии такой оценки расчет WACC не составляет труда, поскольку ставка по займам rD и весовые коэффициенты D/VTA E/ V обьгано известны или легко выводятся из известных показателей8. С оценкой стоимости и требуемой доходности привилегированных акций тоже, как правило, особых сложностей не возникает.
Но когда дело доходит до ценных бумаг другого типа, тут оценка требуемой доходности может вылиться в настоящую проблему. Вот только один пример: конвертируемые облигации, чья доходность для инвесторов частично порождается опционом, позволяющим обменять облигации на акции компании. (Тему конвертируемых ценных бумаг отложим до гл. 23.)
Еще один крепкий орешек — так называемые «мусорные» облигации, которые отличаются очень высоким риском невыполнения обязательств. Чем больше вероятность невыполнения обязательств, тем ниже рыночная цена и тем выше обещанная процентная ставка. Но средневзвешенные затраты на капитал представляют ожидаемую (т. е. среднюю), а отнюдь не обещанную доходность. Скажем, в октябре 2001 г. облигации компании Crown Cork с погашением в 2005 г. продавались всего за 76% от номинала и с обещанной доходностью 18,6%, что на 14 с лишним процентных пункта выше доходности облигаций более приличного инвестиционного класса с таким же сроком погашения. В цене и доходности Crown Cork проявилась серьезная обеспокоенность инвесторов хроническим финансовым нездоровьем компании. Но 18,6% — это не ожидаемая доходность, поскольку в ней не усреднены убытки, к которым привело бы невыполнение обязательств. Присвоить затратам на заемный капитал значение 18,6% при исчислении WACC значило бы существенно завысить подлинные затраты на капитал, свойственные Crown Cork.
Придется вас огорчить: не существует простого или хотя бы сколько-нибудь сподручного приема оценить ожидаемую доходность большинства «мусорных» облигаций9. Впрочем, есть и приятная новость: вообще у большинства облигаций вероятность невыполнения обязательств невелика. Из этого следует, что значения обещанной и ожидаемой доходности довольно близки и обещанную доходность допустимо использовать для расчета средневзвешенных затрат на капитал.
Отраслевые затраты на капитал
Средневзвешенные затраты на капитал можно рассчитывать также для целых отраслей. Допустим, у фармацевтической компании есть подразделение, производящее специальные химические препараты. Какая ставка дисконтирования лучше подходит к проектам этого подразделения — WACC компании или средневзвешенные затраты на капитал, характерные для «портфеля» специализированных производителей химических препаратов? Второй вариант лучше и в принципе, и практически, если есть доступ к достоверным данным о фирмах, сходных с рассматриваемым подразделением параметрами деятельности и рынками.
Практический пример: железнодорожная отрасль.
Каждый год Управление наземного транспорта США (Surface Transportation Board; далее — STB) оценивает затраты на капитал железнодорожной отрасли, определенной как совокупность железных дорог класса I (крупных). Воспользуемся здесь данными и оценками STB, чтобы вычислить WACC железнодорожной отрасли за 1999 г.
Благодаря трудам STB мы располагаем оценками рыночной стоимости железнодорожных обыкновенных акций и всех обращающихся выпусков облигаций, включая такие эквивалентные долгу инструменты, как трастовые сертификаты на оборудование и финансовый лизинг. Агрегированная структура капитала отрасли в интересующем нас году выглядела так:
| Рыночная стоимость ( в млрд дол .) | Весовой коэффициент ( в %) | |
| Долг | 31 627,8 | 37,3 |
| Собственный капитал | 53 210,0 | 62,7 |
Средние затраты на заемный капитал составляли 7,2%. Для оценки затрат на собственный капитал STB пользуется моделью дисконтированного денежного потока с постоянным ростом, которую вам наверняка будет приятно вспомнить (см. разд. 4.3). Если инвесторы ожидают непрерывного роста дивидендов постоянными темпами g, то ожидаемая доходность равна сумме нормы дивидендного дохода и темпов роста:
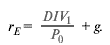
Для инвестора, который приобрел портфель акций железных дорог класса I, в 1999 г. норма дивидендного дохода составляла около 2%. Согласно прогнозам фондовых аналитиков, средние ожидаемые темпы роста прибыли и дивидендов оценивались в 10,9%. Стало быть, затраты на собственный капитал гд= 2,0% + 10,9% = 12,9%.
Включив в расчет предельную ставку корпоративного налога 35%12, получим WACC железнодорожной отрасли:
WACC= 0,072 х (1 – 0,35) х 0,373 + 0,129 х 0,627 = 0,098, или «10%.
Стоимостная оценка компаний: затраты на капитал против денежного потока на акции
Средневзвешенные затраты на капитал обычно используются в качестве предельной (минимально приемлемой) нормы доходности, или ставки дисконтирования, для стоимостной оценки предполагаемых капиталовложений. Но иногда они используются в качестве ставки дисконтирования для стоимостной оценки компании в целом. Так, финансовому менеджеру может потребоваться оценить компанию, намеченную для слияния или поглощения, дабы удостовериться, стоит ли игра свеч.
Стоимостная оценка компаний не таит в себе никаких новых концептуальных проблем. Вы просто подходите к компании как к одному крупному инвестиционному проекту. Прогнозируете денежный поток компании (самая трудная часть процесса) и дисконтируете его к приведенной стоимости. WACC компании являются верной ставкой дисконтирования, если есть основания ожидать, что ее коэффициент долговой нагруз – ки будет достаточно близок к константе. Однако следует помнить несколько фундамен-тальных принципов.
- Принимая WACC за ставку дисконтирования, вы должны прогнозировать денежный поток компании точно так же, как делали бы это для всякого инвестиционного проекта. Не вычитайте проценты. Считайте налоги так, как если бы компания фи нансировалась полностью из собственного капитала. Стоимость налоговой защиты уже включена в формулу WACC.
- Денежный поток компании редко прогнозируется на бессрочную перспективу. Фи нансовые менеджеры обычно устанавливают среднесрочный горизонт прогноза — скажем, 10лет— и прибавляют к денежному потоку последнего года продленную стоимость. Продленная стоимость — это стоимость денежного потока за пределами горизонта прогноза, приведенная к прогнозному периоду. Оценка продленной сто имости требует особенного внимания и осмотрительности, поскольку на нее очень часто приходится основная масса общей стоимости фирмы.
- Дисконтирование по WACC дает оценку активов и операций компании. Если задача состоит в оценке собственного капитала, то есть обыкновенных акций компании, не забудьте вычесть стоимость обращающихся долговых обязательств.
Когда нужно оценить стоимость собственного капитала, есть очевидная альтернатива дисконтированию денежного потока компании по ее WACC: дисконтировать денежный поток на акции, после вычета процентов и налогов, по затратам на собственный капитал. Собственно, эту альтернативу так и называют — метод денежного потока на акции. Если коэффициент долговой нагрузки компании не меняется с течением времени, метод денежного потока на акции дает тот же результат, что и дисконтирование денежного потока компании по WACC с последующим вычитанием стоимости долга.
Метод денежного потока на акции кажется простым, да он такой и есть, когда пропорции долгового и собственного финансирования компании остаются более или менее постоянными на протяжении всей жизни компании. Но затраты на собственный капитал зависят от финансового рычага; они зависят от финансового риска так же, как и от делового риска. Если усилие финансового рычага (долговая нагрузка) в дальнейшем будет существенно меняться, дисконтирование денежного потока на акции по нынешним затратам на собственный капитал ни к чему толковому не приведет.
С единоразовым сдвигом в структуре финансирования еще можно совладать. Взять опять же предполагаемое поглощение. Допустим, финансовый менеджер считает 20%-ный коэффициент долговой нагрузки компании-мишени слишком консервативным и косным — мол, она запросто выдержит и 40% — и просит вас оценить акции компании-мишени исходя из этой предпосылки. К несчастью, в своем расчете затрат на собственный капитал вы использовали нынешний коэффициент 20%. Ничего страшного! Скорректируйте затраты на собственный капитал (в следующем разделе мы напомним, как это делается), а дальше — все как обычно. Разумеется, вы можете сразу прогнозировать и дисконтировать денежный поток на акции исходя из коэффициента долговой нагрузки 40%. И еще вы должны принять за факт, что после поглощения этот коэффициент останется тем же.
Типичные ошибки при использовании формулы WACC
Формула средневзвешенных затрат на капитал очень полезна, но в ней таятся опасные ловушки. Она соблазняет людей на логические ошибки. К примеру, менеджер Q, который ратует за излюбленный проект, смотрит на формулу
WACC= rD(l ~Tc)y + rEy
и думает: «Ага! У моей фирмы прекрасный кредитный рейтинг. Она, если б захотела, могла бы занять, ну скажем, 90% того, что требуется для финансирования проекта. Тогда D/V= 0,9, a E/V= 0,1. Ставка по займам моей фирмы, rD, равна 8%, а требуемая доходность акций, г& — 15%. Стало быть,
WACC= 0,08 х (1 – 0,35) х 0,9 + 0,15 х 0,1 = 0,062, или 6,2%.
С этой ставкой дисконтирования мой проект выглядит грандиозно».
Менеджер Q совершает сразу несколько ошибок. Во-первых, формула средневзвешенных затрат на капитал работает только применительно к проектам, которые являются точной копией самой фирмы. А у фирмы нет долгового финансирования на 90%.
Во-вторых, непосредственный источник финансирования проекта необязательно должен быть связан с предельной доходностью этого проекта. Что тут по-настоящему важно — это вклад проекта в общую кредитоемкость фирмы. Доллар, вложенный в излюбленный проект менеджера Q, не увеличивает кредитоемкость фирмы на 0,90 дол. Если фирма займет 90% от суммы требуемых инвестиций в проект, то в действительности этот долг ляжет отчасти и на ее нынешние активы (а не только на сам проект). Любое преимущество от финансирования нового проекта за счет заимствования сверх нормального уровня нужно относить к старым проектам, а вовсе не к новому.
В-третьих, даже если фирма захочет и сумеет нажать на финансовый рычаг с такой силой, чтобы довести долг до 90%, ее затраты на капитал все равно не снизятся до 6,2% (как следует из расчетов менеджера Q). Вы не можете наращивать долговую нагрузку, не создавая финансового риска для акционеров и, тем самым, не увеличивая гЕ, ожидаемую доходность, которую инвесторы требуют от обыкновенных акций фирмы. К тому же раздувание долга до 90% наверняка поднимет и процентную ставку по займам.

КОРРЕКЦИЯ WACC ПРИ ИЗМЕНЕНИИ ДОЛГОВОЙ НАГРУЗКИ ИЛИ ДЕЛОВЫХ РИСКОВ
Формула WACC предполагает, что оцениваемый проект будет финансироваться из долга и собственного капитала в такой же пропорции, как и фирма в целом. Но что, если эта предпосылка неверна? Что, если уже упоминавшийся проект вечного двигателя способен выдержать долг в размере, скажем, 20% своей стоимости, тогда как доля долгового финансирования фирмы в целом насчитывает 40%?
Сдвиг от 40 к 20% долга меняет значения всех элементов формулы WACC, кроме налоговой ставки13. Изменения весовых коэффициентов очевидны. Но и затраты на собственный капитал, г& становятся меньше вследствие снижения риска. Затраты на заемный капитал, rD, тоже могут сократиться.
На рисунке 19.1 изображена динамика WACC, а также затрат на заемный и собственный капитал, в зависимости от коэффициента долговой нагрузки (в данном случае — отношения долга к собственному капиталу). Горизонтальной линией представлены альтернативные издержки привлечения капитала (г). Помните, что г— это ожидаемая доходность, которую инвесторы требовали бы от проекта, если бы он финансировался полностью из собственного капитала. Альтернативные издержки зависят только от делового риска и в силу этого служат естественной точкой отсчета.
Допустим, компания «Полная чаша» или ее проект вечного двигателя финансируется полностью из собственного капитала (D/V= 0). Бэтой точке WAСС равны затратам на собственный капитал (г^), и оба показателя равны альтернативным издержкам привлечения капитала (г). Начиная с этой точки на рисунке 19.1 по мере увеличения коэффициента долговой нагрузки затраты на собственный капитал растут из-за повышения финансового риска, но WACC— заметьте это! — снижаются. Такое снижение вызвано не использованием «дешевых» заемных средств взамен «дорогостоящего» собственного капитала. Оно вызвано налоговой защитой, которую создают процентные платежи по долгу. В отсутствие корпоративного налога на прибыль средневзвешенные затраты на капитал оставались бы неизменно равны альтернативным издержкам привлечения капитала при любых значениях коэффициента долговой нагрузки. Мы показали это в главах 9 и 17.
Рисунок 19.1.Динамика WACC в зависимости от коэффициента долговой нагрузки. В отсутствие долга WACC равны альтернативным издержкам привлечения капитала. WACC сокращаются по мере наращивания финансового рычага благодаря появлению процентной налоговой защиты
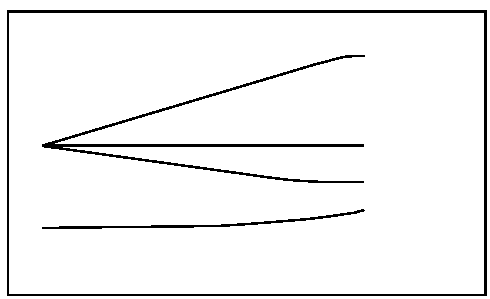
Рисунок 19.1 изображает соотношение между способом финансирования и величиной WACC в наглядном виде, но наши числовые расчеты опираются только на текущий коэффициент долговой нагрузки «Полной чаши» (40%). Мы хотим теперь пересчитать WACC для коэффициента 20%.
Простейший способ состоит из трех действий.
Действие 1. Вычислить альтернативные издержки привлечения капитала. Иными словами, мы должны вычислить WACC и затраты на собственный капитал при нулевом уровне долга. Это действие называют очисткой от долговой нагрузки. Простейшая формула очистки затрат на капитал от долговой нагрузки такова:
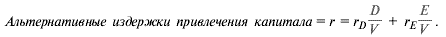
Формула является непосредственным следствием из Первого постулата Модильяни— Миллера (см. разд. 17.1). Если оставить в стороне налоги, средневзвешенные затраты на капитал равны альтернативным издержкам привлечения капитала и не зависят от финансового рычага.
Действие 2. Оценить затраты на заемный капитал, гд, с новым коэффициентом долговой нагрузки и вычислить новую величину затрат на собственный капитал:
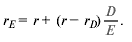
Эта формула является следствием из Второго постулата Модильяни—Миллера (см. разд. 17.2). В ней используется коэффициент D/E, отношение долга к собственному ка – питалу, а не к общей стоимости.
Действие 3. Пересчитать средневзвешенные затраты на капитал с новыми весовыми коэффициентами.
Давайте проделаем это для проекта вечного двигателя при D/V= 0,20, или 20%. Действие 1. Текущий коэффициент долговой нагрузки у компании «Полная чаша» равен D/V= 0,40, так что:
г= 0,08 х 0,4 + 0,146 х 0,6 = 0,12, или 12%.
Действие!. Будем исходить из того, что и при коэффициенте долговой нагрузки 20% затраты на заемный капитал остаются равны 8%. Тогда:
гЕ= 0,12+ (0,12 – 0,08) х 0,25= 0,13, или 13%.
Заметьте, что коэффициент долг/'собственный капитал равен 0,2/0,8 = 0,25. Действие 3. Пересчитать WACC.
WACC= 0,8 х (1 – 0,35) х 0,2 + 0,13 х 0,8 = 0,114, или 11,4%.
Рисунок 19.2 показывает зависимость WACC от коэффициента долговой нагрузки на этом новом числовом материале. При 20%-ном коэффициенте долговой нагрузки (отношении долга к общей стоимости) ставка дисконтирования проекта (11,4%) на 0,56 процентного пункта выше, чем была при 40%-ном коэффициенте.
Рисунок 19.2.График показывает WACC корпорации «Полная чаша» при значениях коэффициента долг/собственный капитал 25 и 67%. Соответствующие значения коэффициента долг/стоимость фирмы— 20 и 40%
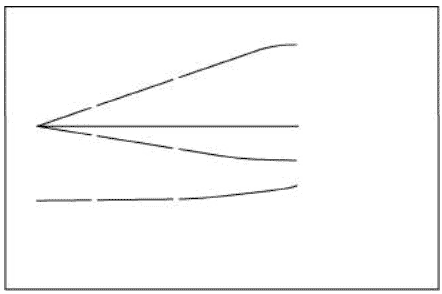
Еще один пример: WACC железнодорожной отрасли при 45% долга.
Давайте вернемся к нашему предыдущему расчету WACC для крупных американских железных дорог. Тот расчет строился на коэффициенте долговой нагрузки (долг/стоимость) 37,3%. А как изменятся WACC железнодорожной отрасли при 45% долга?
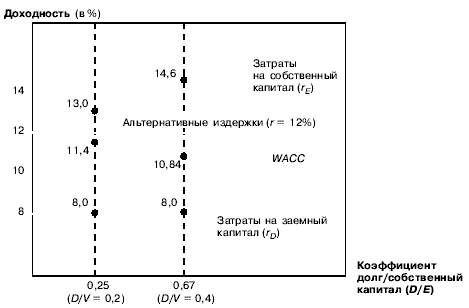
Действие 1. Вычислить очищенные от долговой нагрузки альтернативные издержки привлечения капитала:
г= 0,072 х 0,373 + 0,129 х 0,627 = 0,108.
Действие!. Допустим, при 45% долга затраты на заемный капитал возрастают до 8%. Тогда затраты на собственный капитал:
гЕ= 0,108 + (0,108 – 0,080) х 45/55 = 0,13.
Действие 3. Пересчитать WACC Если предельная ставка налога по-прежнему равна 35%, то:
WACC= 0,080 х (1 – 0,35) х 0,45 + 0,130 х 0,55 = 0,095, или 9,5%.
Затраты на капитал уменьшаются почти на половину процентного пункта. Хорош выигрыш? Не так хорош, как кажется. В этом простом числовом примере затраты на капитал сокращаются по мере наращивания финансового рычага, но только благодаря процентной налоговой защите. В главе 18 мы тщательно разобрали причины, почему учет процентной налоговой защиты как таковой (в узком контексте) приводит к завышенной оценке преимуществ долга. Скажем, издержки финансовых трудностей, сопряженные с высоким уровнем долга, никак не проявляются в формуле WACC или в стандартных формулах, описывающих затраты на собственный капитал в связи с финансовым рычагом.
Бета без долговой нагрузки и с обновленной долговой нагрузкой
Описанная нами процедура из трех действий позволяет (1) очистить от долговой нагрузки затраты на собственный капитал и (2) придать им новую долговую нагрузку. Некоторым финансовым менеджерам кажется удобнее и проще проделывать эти манипуляции с бетой акций. Когда известна бета акций при новом коэффициенте долговой нагрузки, затраты на собственный капитал определяются с помощью модели оценки долгосрочных активов. После чего легко пересчитать WACC
Формула беты, очищенной от долговой нагрузки, приводилась в разделе 9.3:
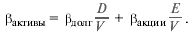
Согласно этой формуле, бета активов фирмы воплощается в бете портфеля всех ее обращающихся ценных бумаг (долговых обязательств и акций). Инвестор, купивший такой портфель, автоматически завладел бы активами, принимая на себя только деловой риск.
Формула придания бете новой долговой нагрузки, по сути, воспроизводит Второй постулат ММ, разве что там вместо беты фигурирует доходность:
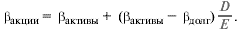
Восстановление пропорций
В формуле WACC, как и в формулах ожидаемой доходности без долговой нагрузки и с обновленной долговой нагрузкой, нет ничего сложного, только нужно всегда помнить о предпосылках, на которые они опираются. Самая важная из них — восстановление пропорций.
Расчет WACC компании при ее нынешней структуре капитала требует непременного соблюдения условия, что эта структура капитала неизменна; иными словами, в обозримом будущем компания должна поддерживать структуру капитала в таких пропорциях, чтобы ее коэффициент долговой нагрузки, исчисленный по рыночной стоимости, оставался одинаковым. Взять хотя бы ту же корпорацию «Полная чаша». Изначально ее коэффициент долговой нагрузки составляет 40% при общей рыночной стоимости 125 млн дол. Внезапно продукты компании начинают пользоваться таким успехом на рынке, что ее рыночная стоимость возрастает до 150 млн дол. Восстановление пропорций означает, что компания должна теперь увеличить долг до 0,4 х 150 млн дол. = 60 млн дол.15, вновь подтянув коэффициент долговой нагрузки к 40%. Если бы рыночная стоимость, наоборот, снизалась, «Полная чаша» должна была бы погасить соответствующую часть долга.
Разумеется, в реальной жизни восстановление пропорций происходит не такими резкими рывками. Для практических целей вполне достаточно постепенных, но неукоснительных коррективов, мало-помалу приближающих к долгосрочному целевому нормативу. Но если фирма планирует серьезный сдвиг в структуре капитала (например, если она намерена полностью погасить имеющийся долг), формула WACC перестает работать. В подобных случаях следует пользоваться методом APV, к которому мы и обратимся в следующем разделе.
Наша трехэтапная процедура пересчета WACC опирается на сходную предпосылку восстановления пропорций16. Предполагается, что фирма всегда будет поддерживать изначальный коэффициент долговой нагрузки. Кроме того, в действиях 1 и 2 (очистка от долговой нагрузки и придание новой долговой нагрузки) совершенно не учитывается возможное влияние личного подоходного налога, уплачиваемого инвесторами, на величину затрат на заемный и собственный капитал.
СКОРРЕКТИРОВАННАЯ ПРИВЕДЕННАЯ СТОИМОСТЬ
Давайте теперь познакомимся с другим подходом. Вместо того чтобы возиться со ставкой дисконтирования, мы можем внести поправки непосредственно в оценку денежного потока и приведенной стоимости издержек или выгод финансирования. Этот подход так и называют: метод скорректированной приведенной стоимости (APV).
Суть метода скорректированной приведенной стоимости легче всего постичь на простых числовых примерах. Мы начнем с анализа проекта при базовых предпосылках, а затем рассмотрим возможные побочные эффекты финансирования проекта в случае его принятия.
Базовая оценка
Метод скорректированной приведенной стоимости начинается с оценки проекта как мини-фирмы, которая финансируется целиком из собственного капитала. Возьмем для примера проект производства солнечных батарей. Проект требует 10 млн дол. инвестиций и сулит равномерный посленалоговый денежный поток объемом 1,8 млн дол. в год на протяжении 10 лет. Альтернативные издержки привлечения капитала составляют 12%; эта величина отражает деловой риск проекта. От акций такой мини-фирмы инвесторы стали бы требовать ожидаемую доходность 12%.
Отсюда базовая оценка чистой приведенной стоимости нашей мини-фирмы:
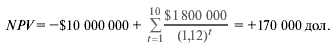
Учитывая масштабы проекта, эта величина почти не отличается от нуля. В мире ММ, где решения по финансированию не имеют значения, финансовый менеджер мог бы согласиться принять проект, но мог бы без малейшего сожаления и отказаться от него.
Эмиссионные издержки
Но допустим, фирма должна финансировать 10 млн дол. инвестиций за счет выпуска акций (будь проект отвергнут, ей не пришлось бы выпускать акции) и эмиссионные издержки поглотят 5% валовых поступлений от выпуска. Значит, для того чтобы получить в руки 10 млн дол., фирме нужно выпустить акции на 10 526 000 дол. Разница в размере 526 тыс. дол. пойдет на оплату услуг подписчиков, юристов и других лиц, причастных к эмиссии.
Вычтя эмиссионные издержки из базовой чистой приведенной стоимости, находим скорректированную приведенную стоимость:
APV= базоваяNPV – эмиссионные издержки= +$170 000 – $526 000= -356 000 дол.
Фирма должна отказаться от проекта, поскольку скорректированная приведенная стоимость имеет отрицательное значение.
Увеличение кредитоемкости фирмы
Рассмотрим различные сценарии финансирования. Предположим, что фирма придерживается нормативного коэффициента долговой нагрузки 50%, то есть ограничивает долю долга 50% стоимости своих активов. Стало быть, инвестируя больше, она и занимает больше; в этом смысле инвестиции увеличивают кредитоемкость фирмы.
Обладает ли кредитоемкость какой-нибудь ценностью? Наиболее распространенный ответ — да, обладает, благодаря налоговой защите, которую создают процентные платежи по корпоративным займам. (Возможно, вы захотите обновить в памяти наше обсуждение темы долга и налогов в гл. 18.) Например, согласно теории ММ, стоимость фирмы не зависит от ее структуры капитала, если не считать приведенную стоимость процентной налоговой защиты:
Стоимость фирмы = стоимость при финансировании из собств. капитала + PVналог.защита
Эта теория учит нас исчислять стоимость фирмы в два действия. Сначала надо найти базовую стоимость при условии финансирования полностью из собственного капитала, а затем к полученному результату прибавить приведенную стоимость налогов, сэкономленных вследствие отхода от политики финансирования только из собственного капитала. Такая процедура представляет собой расчет APV для фирмы в целом.
Мы можем повторить те же вычисления и для отдельного проекта. Например, проект производства солнечных батарей увеличивает стоимость активов фирмы на 10 млн дол. и тем самым побуждает фирму занять еще 5 млн дол. Для упрощения допустим, что этот заем погашается равными порциями, так что сумма долга уменьшается по мере амортизационного списания балансовой стоимости проекта. Допустим также, что процентная ставка по займу составляет 8%. В таблице 19.1 показано, как вычислить стоимость процентной налоговой защиты. Это и есть стоимость дополнительной кредитоемкости фирмы, которую создает проект. Прибавив эту величину к чистой приведенной стоимости проекта, получим скорректированную приведенную стоимость:
APV= базовая NPV+ РУналогзащта = +$170 000+ $576 000= 746 000 дол.
С такими цифрами проект производства солнечных батарей выглядит вполне приемлемо. Однако обратите внимание на разницу между этим расчетом APV и расчетом NPVc использованием WACC в качестве ставки дисконтирования. В расчет APV заложена предпосылка, что долг, равный 50% балансовой стоимости, погашается по фиксированному графику. В расчете NPV с использованием WACC долг принимается за постоянную долю от рыночной стоимости проекта в каждый год его жизненного цикла. Поскольку стоимость проекта в отдельные годы неизбежно окажется выше или ниже ожидаемой, использование WACC предполагает также, что в дальнейшем уровень долга будет с необходимостью повышаться или понижаться, дабы коэффициент долговой нагрузки оставался постоянным.
Метод APV применим в тех случаях, когда долг, поддерживаемый проектом, привязан к балансовой стоимости проекта или когда этот долг нужно погашать по фиксированному графику. Так, Каплан и Рубак воспользовались методом APV для анализа цен в выборке сделок по выкупу компаний за счет займа. Такие сделки — это поглощения, обычно зрелых фирм, финансируемые преимущественно из долга. Однако новый (возросший) уровень долга не обязательно должен сохраняться вовеки. Бизнес-планы в рамках выкупов за счет займа намечают пути привлечения дополнительных денежных средств — в частности, через распродажу активов, снижение издержек или повышение нормы прибыли. Эти дополнительные средства направляются на погашение долга, из которого финансировалась сделка. В силу этого вы не можете использовать WACC в качестве ставки дисконтирования при оценке выкупов за счет займа, так как коэффициенты долговой нагрузки в таких случаях не постоянны.
А вот метод APV прекрасно подходит для оценки выкупов за счет займа. Сперва стоимость компании определяется так, словно бы финансирование осуществлялось целиком из собственного капитала. Это означает, что денежный поток прогнозируется в посленалоговом выражении, но без учета какой-либо налоговой защиты, создаваемой займами, которые обеспечивают выкуп. Налоговая защита оценивается отдельно. Устанавливается график погашения долга (примерно такой, какой показан в табл. 19.1), на его основе вычисляется приведенная стоимость процентной налоговой защиты, и затем полученная величина прибавляется к стоимости, рассчитанной при условии финансирования из собственного капитала. Сюда же прибавляются и всякие другие побочные эффекты финансирования. В итоге получаем скорректированную приведенную стоимость компании19. Как обнаружили Каплан и Рубак, метод ЛРКпревосходно объясняет цены наиболее заметных поглощений, даже несмотря на то что отнюдь не вся информация, известная участникам торгов, получает публичную огласку. Самим Кап-лану и Рубаку в своем анализе пришлось ограничиться данными, открытыми для массового доступа.
Таблица 19.1 Расчет приведенной стоимости процентной налоговой защиты по долгу, связанному с проектом производства солнечных батарей (числовые данные— втыс.дол.)
| Год | Долг в обращении на начало года | Проценты | Процентная налоговая защита | Приведенная стоимость налоговой защиты |
| 1 2 3 4 5 6 7 8 9 10 |
5000 4500 4000 3500 3000 2500 2000 1500 1000 500 |
400 360 320 280 240 200 160 120 80 40 |
140 126 112 98 84 70 56 42 28 14 |
129.6 108.0 88.9 72.0 57.2 44.1 32.6 22.7 14.0 6.5 Итого:576 |
Стоимость процентной налоговой защиты
В таблице 19.1 мы сделали смелое допущение, что фирма способна полностью реализовать процентную налоговую защиту в размере 0,35 дол. на каждый доллар процентных платежей. Кроме того, мы подошли к процентной налоговой защите как к надежному денежному потоку, который можно дисконтировать по низкой ставке 8%.
Истинная приведенная стоимость налоговой защиты в нашем примере почти наверняка меньше 576 тыс. дол. Тому есть несколько причин.
- Вы не сумеете воспользоваться налоговой защитой, если не платите налогов, и вы не платите налогов, если не зарабатываете денег. Очень немногие фирмы могут быть твердо уверены, что их будущих прибылей окажется достаточно, чтобы пользоваться процентной налоговой защитой.
- Правительство дважды «отщипывает куски» от корпоративной прибыли: через соб ственно корпоративный налог и через личный подоходный налог, взимаемый с дер жателей облигаций и акций. Корпоративный налог благоприятствует долговому фи нансированию; личный подоходный налог — финансированию из собственного ка питала (акций).
- Кредитоемкость проекта зависит от того, насколько успешно он реализуется. Когда прибыль превосходит ожидания, фирма может занимать больше; когда дела идут плохо, проект вообще не выдержит никакого долга. Если будущая величина долга привязана к будущей стоимости проекта, то значения налоговой защиты, представ ленные в таблице 19.1, — это всего лишь приблизительные оценки, но никак не твер до определенные величины.
В главе 18 мы уже говорили о том, что эффективная налоговая защита по долгу (обозначаемая Т*) может оказаться меньше 35% (Тс = 0,35). Но мы так и не установили точную величину Т*.
Предположим к примеру, что Т* = 0,25. Мы легко можем пересчитать скорректированную приведенную стоимость проекта производства солнечных батарей: просто умножим приведенную стоимость процентной налоговой защиты на 25/35. Итоговая величина в таблице 19.1 уменьшается с 576 000 до 411 000 дол. (= 576 000 дол. х 25/35). Скорректированная приведенная стоимость снижается:
APV= базовая NPV+ РГналот защита = +$170 000+ $411000= 581000 дол.
Приведенная стоимость налоговой защиты будет еще меньше, если подходить к налоговой защите как к прогнозному денежному потоку и дисконтировать по более высокой ставке. Допустим, фирма увязывает величину долга с фактическим денежным потоком от проекта. Тогда процентная налоговая защита становится такой же рискованной, как и сам проект, и ее следует дисконтировать по ставке 12%, соответствующей альтернативным издержкам привлечения капитала. При Т* = 0,25 приведенная стоимость налоговой защиты падает до 362 тыс. дол.
Обзор метода скорректированной приведенной стоимости
Если решение инвестировать в капитальный проект оказывает значительные побочные эффекты на другие решения фирмы по финансированию, то эти побочные эффекты тоже следует учитывать в стоимостной оценке проекта. К ним относятся процентная налоговая защита по долгу, обусловленному проектом (плюс), любые эмиссионные издержки, связанные с привлечением финансовых ресурсов для проекта (минус), и прочие возможные эффекты, такие, в частности, как правительственные возвратные субсидии под проект.
Идея, лежащая в основе метода скорректированной приведенной стоимости, сво-дится к принципу «разделяй и властвуй». Этот метод не охватывает все побочные эффекты в одном расчете. Напротив, он предусматривает серию последовательных вычислений приведенной стоимости. Сначала дается базовая оценка стоимости проекта как отдельной мини-фирмы, финансируемой только из собственного капитала. Затем определяются важные побочные эффекты финансирования и вычисляется приведенная стоимость издержек или выгод, которые они несут фирме. И наконец, все полученные приведенные стоимости складываются, чтобы оценить общий вклад проекта в стоимость фирмы. Итак, в общем виде:
APVnpoeKI = базовая NPV+ сумма приведенных стоимостей побочных эффектов проекта.
Толковый финансовый менеджер захочет узнать не только величину скорректированной приведенной стоимости, но и откуда она возникает. Положим, базовая чистая приведенная стоимость имеет положительное значение, но издержки выпуска акций для финансирования проекта перевешивают связанные с ним выгоды. Это заставит менеджера оглядеться в поисках альтернативного финансового плана, который мог бы спасти проект.
APV в международных проектах
Метод скорректированной приведенной стоимости особенно полезен, когда побочных эффектов финансирования много и когда они играют важную роль. Такое часто бывает с крупными международными проектами, для которых разрабатываются специальные схемы проектного финансирования и заключаются специальные контракты с поставщиками, потребителями и правительствами20. Вот лишь несколько примеров побочных эффектов финансирования, возникающих на международной арене.
Тему проектного финансирования мы затронем в главе 25. Обычно оно начинается с очень высокого коэффициента долговой нагрузки, так что основная масса, а то и весь денежный поток от проекта на ранних стадиях уходит на обслуживание долга. Инвесторам в акции приходится ждать своей очереди. А поскольку высокий коэффициент долговой нагрузки не останется постоянным, здесь следует пользоваться методом APV.
Проектное финансирование порой включает в себя займы по благоприятным процентным ставкам. Многие правительства субсидируют экспорт через специальные финансовые программы, а поставщики производственного оборудования нередко готовы предоставлять кредиты, тем самым помогая себе и своим клиентам завершить сделку купли-продажи. Допустим к примеру, что ваш проект требует строительства энергостанции в какой-то определенной местности. Вы рассматриваете предложения поставщиков из разных стран. Не удивляйтесь, если окажется, что конкурирующие поставщики наперебой стараются «подсластить» свои предложения кредитами с низким процентом или возможностью долгосрочной аренды (лизинга) оборудования на привлекательных условиях. Вам следует вычислить NPV таких кредитов и лизинга, а затем ввести эти оценки в ваш анализ проекта.
Иногда международные проекты подкрепляют особыми контрактами с поставщи
ками или потребителями. Предположим, производитель хочет обеспечить себе надеж
ную линию поставок важнейшего сырья — скажем, жженой магнезии. Такой произво
дитель может субсидировать строительство новой обжиговой печи, согласившись заку
пать 75% продукции и гарантировав минимальную закупочную цену. Такая гарантия —
это, несомненно, ценная «добавка» к ЛРКпроекта: даже если мировые цены на жже
ную магнезию упадут ниже оговоренного минимума, проект все равно не пострадает.
Вы должны оценить стоимость такой гарантии (методами, которые будут изложены в
гл.20 и 21) и прибавить ее к APV.
Иногда местные правительства налагают ограничения (в виде дополнительных из – ~w~
держек и в неденежной форме) на инвестиции или, наоборот, сворачивание капиталовложений. Например, правительство Чили, пытаясь замедлить массовый приток краткосрочного капитала на местный рынок в 1990-х годах, потребовало от инвесторов «замораживания» части их инвестиционных доходов на непроцентных банковских счетах сроком до двух лет. Любому инвестору в Чили в тот период следовало рассчитать издержки этого требования и вычесть их из APV.
APVB проекте вечного двигателя
Может показаться, что две описанные процедуры стоимостной оценки — дисконтирование по WACC и расчет APV— не имеют между собой никаких точек соприкосновения. Однако мы готовы продемонстрировать, что при согласованных предпосылках обе они дают примерно одинаковые результаты. Давайте удостоверимся в этом на примере проекта вечного двигателя из раздела 19.1.
В дальнейших вычислениях мы оставим в стороне любые эмиссионные издержки и сосредоточимся на стоимости процентной налоговой защиты. Ради простоты допустим здесь, что единственным побочным эффектом финансирования является именно налоговая защита по долгу, обусловленному проектом вечного двигателя, и будем рассматривать только корпоративный налог (другими словами, 7* = Тс). Как и в разделе 19.1, возьмем за предпосылку, что по деловому риску и способу финансирования проект вечного двигателя полностью совпадает со своей материнской компанией «Полная чаша».
Продисконтировав посленалоговый денежный поток проекта (1,355 млн дол.) по альтернативным издержкам привлечения капитала (г =12%) и затем вычтя из полученной величины 12,5 млн дол. капиталовложений, находим базовую чистую приведенную стоимость. Для бессрочного денежного потока это выглядит так:
$1355 000
Базовая NPV= -$12 500 000+ $1355 000/0.12 =-1,21 млн дол.
Стало быть, при финансировании только из собственного капитала проект никудышный. Однако на самом деле проект поддерживает 5 млн дол. долга. Если ставка по займам составляет 8% (гл = 0,08), а налоговая ставка— 35% (7^ = 0,35), то годовая процентная налоговая защита насчитывает 0,35 х 0,08 х 5 млн = 0,14 млн, или 140 000 дол. Сколько стоит такая налоговая защита? Это зависит от того, каким финансовым правилом руководствуется компания.
- Финансовое правило 1: фиксированный долг. Занимать определенную долю изначаль ной стоимости проекта и делать любые выплаты в погашение долга по заранее уста новленному графику. Мы следовали этому правилу в таблице 19.1.
- Финансовое правило 2: пропорциональный (или переменный) долг. Корректировать ве личину долга в каждом будущем периоде так, чтобы поддерживать его в постоянной пропорции к будущей стоимости проекта.
Что значит каждое из этих правил для проекта вечного двигателя? По финансовому правилу 1, долг в любых обстоятельствах остается равным 5 млн дол., и процентная налоговая защита по-прежнему насчитывает 140 тыс. дол. в год. Эта налоговая защита связана с фиксированными процентными платежами, поэтому в качестве ставки дисконтирования вполне оправданно использовать затраты на заемный капитал 8%:
PVналог. защита(фиксированный долг) = $140 000 / 0,08 = 1 750 000 дол.
APV= базовая NPV+ PVналог. защита= -$1210 000+ $1750 000= +540 000 дол.
Если бы строительство вечного двигателя финансировалось исключительно из собственного капитала, стоимость проекта составляла бы 11,29 млн дол. С 5 млн дол. фиксированного долга стоимость проекта увеличивается на приведенную стоимость налоговой защиты до 11,29 млн дол. + 1,75 млн дол. = 13,04 млндол.
По финансовому правилу 2, величина долга поддерживается в постоянной пропорции 40% к фактической стоимости проекта. Это означает, что на начальной стадии реализации проекта будущие уровни долга еще неизвестны. Они могут быть выше или ниже в зависимости от успеха или неудачи проекта. Стало быть, процентная налоговая защита принимает на себя деловой риск проекта.
Если процентной налоговой защите присущ такой же риск, как и самому проекту, ее следует дисконтировать по альтернативным издержкам финансирования проекта, то есть в данном случае по ставке 12%:
PVналог. защита(фиксированный долг) = $140 000 / 0,12 = 1 170 000 дол.
APV= -$1 210 000 + $1 170 000 = -40 000 дол.
Теперь у нас есть три разные оценки проекта вечного двигателя:
- APV (фиксированный долг) = +0,54 млндол.;
- APV (пропорциональный долг) = —0,04 млндол.;
- NPV (дисконтированная по WACC) = 0.
Первая APV имеет самую большую величину, поскольку исчислена при условии, что долг фиксированный, а не пропорциональный, и значит, налоговая защита настолько же надежна, как и порождающие ее процентные платежи.
Но почему оценки чистой приведенной стоимости из второго и третьего пунктов, обе из которых опираются на финансовое правило 2, не совпадают? Потому что в нашем расчете APV при условии пропорционального долга финансовое правило 2 соблюдено только отчасти.
Даже в случае с пропорциональным долгом процентная налоговая защита следующего года фиксирована. Процентная налоговая защита в году 1 определена величиной долга на дату 0 (начало проекта). Значит, процентную налоговую защиту первого года следовало бы дисконтировать по ставке 8, а не 12%.
Процентная налоговая защита в году 2 на начальной стадии проекта неизвестна, поскольку в дату 1 величина долга будет скорректирована в зависимости от успехов реализации проекта за первый год. Но как только уровень долга на дату 1 установлен, выясняется и величина процентной налоговой защиты. Следовательно, прогнозируемую к дате 2 налоговую защиту (140 тыс. дол.) нужно дисконтировать за один год по ставке 12%, а еще за один — по ставке 8%.
Итак далее. Каждый год, едва лишь восстановлена надлежащая пропорция долга, процентная налоговая защита становится фиксированной. Скажем, величина процентной налоговой защиты в году 15 фиксируется, как только происходит корректировка долга в году 14. Стало быть, приведенная стоимость налоговой защиты в году 15 равна ее прогнозной величине на дату 0 (все те же 140 тыс. дол.), дисконтированной за один год по ставке 8% и за остальные 14 лет по ставке 12%.
Таким образом, строгая процедура исчисления точной стоимости налоговой защиты при соблюдении финансового правила 2 такова:
- дисконтировать прогнозную величину по альтернативным издержкам привлечения капитала, ибо налоговая защита будущих лет привязана к фактическим денежным потокам;
- умножить найденную приведенную стоимость на (1 + r)/(l + rD), ибо процентная налоговая защита приобретает определенность на один период раньше, чем фактически наступает.
Для проекта вечного двигателя налоговая защита прогнозируется в размере 140тыс., или 0,14 млн дол. Вот ее точная стоимость:
PV(приблизительная оценка) = $1 400 000 / 0.12= 1 170 000 дол.;
PV(точная оценка) = $1 170 000 х 0.12 / 0.08 = 1 210 000 дол.
При данных предпосылках относительно будущей кредитоемкости APV проекта равна:
APV= базовая NPV+ PVналог. защита = -$1210 000+ $1210 000= 0.
Этот результат полностью совпадает с нашей изначальной оценкой проекта вечного двигателя, выполненной на основе WACC. Дисконтирование по WACC подспудно предполагает, что налоговая защита следующего года определяется долгом текущего года.
На практике редко имеет смысл всерьез заботиться о том, приблизительно или точно оценена налоговая защита (в первом случае APV= —0,04 млн дол., во втором APV= 0). Лучше не пожалейте времени и забот на уточнение прогноза денежного потока и на анализ сценариев («что будет, если…»).
Какое из двух финансовых правил лучше?
Но вот какое из финансовых правил предпочтительнее — фиксированный долг или пропорциональный долг?
Иногда долг нужно погашать по фиксированному графику, как в проекте производства солнечных батарей (см. табл. 19.1). Это особенность и большинства выкупов за счет займа. Однако в типичном случае мы склоняемся к восстановлению пропорций, то есть к финансовому правилу 2. Всякое бюджетное планирование, опирающееся на предпосылку, что уровень долга всегда останется постоянным, получается чрезмерно упрощенным. Должны ли мы исходить из того, что проект вечного двигателя увеличивает кредитоемкость фирмы на 5 млн дол. не только на первых порах, но отныне и вовеки? Это все равно, как сказать, что будущая стоимость проекта никогда не изменится, — пожалуй, слишком смелое допущение.
В общем, финансовое правило 2 лучше: не «Всегда занимайте 5 млн дол.», а «Всегда занимайте 40% стоимости проекта вечного двигателя». Тогда с увеличением стоимости проекта фирма занимает больше. Если же стоимость сокращается, фирма занимает меньше. При такой политике вы уже не можете дисконтировать будущую процентную налоговую защиту по ставке заимствования, ибо налоговая защита утрачивает определенность. Ее величина зависит от фактического уровня долга и, следовательно, от фактической будущей стоимости проекта.
APV и предельная норма доходности
Величина APV говорит нам о том, вносит ли проект чистый вклад в стоимость фирмы. Она также может подсказать нам, каким должен быть безубыточный денежный поток или внутренняя норма доходности проекта. Давайте опять обратимся к проекту вечного двигателя, дабы удостовериться в этом. Сперва подсчитаем прибыль, при которой APV= 0. После чего определим минимально приемлемую внутреннюю норму доходности проекта (IRR).
APV = годовая прибыль / r – инвестиции + PVналог. защита = годовая прибыль / 0,12 – $ 12 500 000 + $ 1 210 000 = 0
Годовая прибыль = 1 355 000 дол.
или 10,84% от 12,5 млн дол. капиталовложений. Иными словами, минимально приемлемая IRR проекта равна 10,84%. При этой IRR величина APV проекта сводится к нулю.
Представим себе другой проект с бессрочным денежным потоком. Его альтернативные издержки привлечения капитала такие же (г= 0,12), и он тоже увеличивает кредитоемкость фирмы на 40% стоимости проекта. Мы уже знаем, что если у такого проекта IRR окажется выше 10,84%, то его APV будет иметь положительное значение. Следовательно, мы можем сократить анализ, просто продисконтировав денежный поток проекта по ставке 10,84%22. Эта ставка дисконтирования представляет собой скорректированные затраты на капитал. Она отражает как деловой риск проекта, так и его вклад в общую кредитоемкость фирмы.
Обозначим скорректированные затраты на капитал г*. Для того чтобы вычислить г*, мы должны найти минимально приемлемую внутреннюю норму доходности (IRR), при которой APV= 0. Общее правило таково: принимать проекты, которые имеют положительную NPV при скорректированных затратах на капитал г*.
Общее определение скорректированных затрат на капитал
Скорректированные затраты на капитал 10,84% в проекте вечного двигателя идентичны (не удивляйтесь!) WACC корпорации «Полная чаша», которые мы вычислили в разделе 19.1.
Суммируем две концепции затрат на капитал.
- Концепция 1: альтернативные издержки привлечения капитала (г). Это ожидаемая до ходность, которую обеспечивают активы с эквивалентным риском на рынках капи тала. Она зависит от риска, присущего денежному потоку проекта. Альтернативные издержки служат подходящей ставкой дисконтирования для проекта, финансируе мого полностью из собственного капитала.
- Концепция 2: скорректированные затраты на капитал (г*). Это скорректированные альтернативные издержки, или предельная норма доходности, которая отражает по бочные эффекты финансирования инвестиционного проекта.
Некоторые люди говорят просто «затраты на капитал». Иногда из контекста ясно, что они имеют в виду. Но порой они сами не знают, к какой концепции апеллируют, и это может вызвать полную неразбериху.
Когда побочные эффекты финансирования важны, следует принимать проекты с положительной APV Но если вы знаете скорректированную ставку дисконтирования, вам нет нужды вычислять APV. просто считайте NPVno скорректированной ставке. Формула средневзвешенных затрат на капитал — это самый общий способ получить скорректированные затраты на капитал.
ДИСКОНТИРОВАНИЕ НАДЕЖНОГО НОМИНАЛЬНОГО ДЕНЕЖНОГО ПОТОКА
Предположим, вы подумываете о покупке оборудования ценой 100 тыс. дол. Производитель предлагает вам заманчивую сделку: финансировать покупку кредитом на пять лет под 5% годовых. Банку за такой заем вам пришлось бы заплатить 13%. Ваша предельная налоговая ставка составляет 35% (Тс= 0,35).
Сколько стоит этот кредит? Если вы им воспользуетесь, денежный поток будет таким (в тыс. дол):
| Период | 0 | 1 | 2 | 3 | 4 | 5 |
| Денежный поток | 100 | -5 | -5 | -5 | -5 | -105 |
| Налоговая защита | +1,75 | +1,75 | +1,75 | +1,75 | +1,75 | |
| Посленалоговый денедный поток | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -103,25 |
А какой должна быть ставка дисконтирования?
Здесь вы имеете дело с надежным номинальным денежным потоком — надежным, потому что ваша компания, взяв кредит, обязана погасить его23, и номинальным, потому что величина выплат зафиксирована независимо от инфляции. Ну а верная ставка дисконтирования для надежных номинальных денежных потоков — это послена-логовая процентная ставка вашей компании по «^субсидируемым займам24. В данном случае г* = rD(\ – Тс) = 0,13(1 – 0,35) = 0,0845. Отсюда:
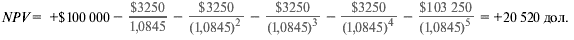
Производитель, по существу, снизил покупную цену оборудования с 100 тыс. дол. до 100 000 дол. — 20 520 дол. = 79 480 дол. Теперь вы можете вернуться назад и пересчитать чистую приведенную стоимость оборудования с этой соблазнительной ценой либо вы можете использовать чистую приведенную стоимость субсидируемого кредита как элемент скорректированной приведенной стоимости оборудования.
Очевидно, мы должны теперь объяснить, почему г* = rD(\ — Тс) — это подходящая ставка дисконтирования для надежных номинальных денежных потоков. Неудивительно, что г* зависит от гд, ставки по несубсидируемым займам, так как это альтернативные издержки инвесторов — процентная ставка, которую они требовали бы от долговых обязательств вашей компании. Но почему rD должна быть выведена в посленалоговом выражении?
Для простоты давайте рассмотрим однолетний субсидируемый кредит в размере 100 тыс. дол. по ставке 5%. Сопряженный с ним денежный поток выглядит следующим образом (в тыс. дол.):
| Период 0 | Период 1 | |
| Денежный поток | 100 | -105 |
| Налоговая защита | + 1,75 | |
| Посленалоговый денежный поток | 100 | -103,25 |
Теперь зададимся вопросом: «Какую максимальную сумму X вы могли бы занять на 1 год по обычным каналам, если на обслуживание долга отведено 103 250 дол.?».
«Занять по обычным каналам» — значит под 13% в доналоговом выражении или под 8,45% в посленалоговом выражении. Стало быть, для выплаты основной суммы долга и процентов в посленалоговом исчислении вам нужно иметь в своем распоряжении 108,45% суммы займа. Если 1,0845Х= 103 250, то Х= 95 205. Коль скоро вы в состоянии занять 100 тыс. дол. в форме возвратной субсидии и только 95 205 дол. по обычным каналам, разность (4795 дол.) остается в вашем кармане, а следовательно, это и есть чистая приведенная стоимость вашего однолетнего субсидированного кредита.
Когда вы дисконтируете надежный номинальный денежный поток по посленалого-вой ставке заимствования, вы тем самым вычисляете эквивалентный заем — сумму, которую вы могли бы взять в долг по обычным каналам, используя соответствующий денежный поток для обслуживания долга. Заметим, что
Эквивалентный заем = РV (денежный поток для обслуживания долга) = $103 250 / $1.0845 = 95 205 дол.
В некоторых случаях это легче понять, поставив себя на место кредитора, а не заемщика. Например, вы можете спросить себя: «Сколько моей компании пришлось бы инвестировать сегодня, чтобы справиться с обслуживанием субсидируемого кредита в следующем году?». Ответ— 95 205 дол.: если вы ссужаете такую сумму под 13%, то заработаете на этом 8,45% в посленалоговом выражении и, следовательно, получите 95 205 дол. х 1,0845 = 103 250 дол. Этой сделкой вы фактически «сводите к нулю» свои будущие обязательства. Если вы способны взять взаймы 100 тыс. дол. и отложить на обслуживание кредита только 95 205 дол., у вас явно остается 4795 дол., которые вы можете тратить по своему усмотрению. Эта величина представляет собой чистую приведенную стоимость субсидированного кредита.
Стало быть, с какой позиции — заемщика или кредитора — ни посмотреть, выходит, что верной ставкой дисконтирования для надежного номинального денежного потока является посленалоговая процентная ставка
В определенном смысле это очевидный вывод. Компании вольны брать в долг или давать взаймы. Если они ссужают деньги, то получают посленалоговый процент на свои инвестиции; если они занимают деньги на рынке капитала, то платят по долгу посленалоговый процент. Таким образом, альтернативные издержки компании, инвестирующей средства в эквивалентный долгу денежный поток, равны посленалоговой процентной ставке. Это и есть скорректированные затраты на капитал для эквивалентных долгу денежных потоков.
Приведем еще несколько примеров эквивалентного долгу денежного потока.
Предположим, вы заключаете договор на техническое обслуживание с лизинговой фирмой, предоставляющей автомобили в аренду. Фирма согласна поддерживать ваш автомобиль в хорошем рабочем состоянии на протяжении следующих двух лет за ежемесячную фиксированную плату. Такие платежи образуют эквивалентный долгу денежный поток.
Проекты капиталовложений обычно оцениваются
дисконтированием ожидаемых от них совокупных посленалоговых денежных потоков. Налоговая защита, создаваемая амортизационными отчислениями, увеличивает денежный поток проекта, но ее не учитывают отдельно; ее просто «встраивают» в общую оценку наряду с десятками и даже сотнями других специфических притоков и оттоков денежных средств. Альтернативные издержки проекта отражают средний риск этого агрегированного денежного потока.
Тем не менее вы, положим, все же хотите узнать, сколько стоит амортизационная налоговая защита сама по себе. У фирмы, которая уверена, что ей будет из чего платить налоги, амортизационная налоговая защита представляет собой надежный номиналь – ный поток. Следовательно, дисконтировать ее надо по посленалоговой ставке заим-ствования.
Посленалоговая ставка дисконтирования равна г^(1 — Тс) = 0,13(1 — 0,35) = 0,0845. (Мы по-прежнему исходим из того, что доналоговая ставка по займам составляет 13%, а предельная ставка корпоративного налога— 35%.) Отсюда приведенная стоимость налоговой защиты: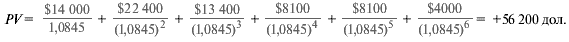
Согласуется ли наша процедура оценки эквивалентных долгу денежных потоков с изложенными выше методами WACC и APV? Да, согласуется, и теперь мы это наглядно продемонстрируем.
Давайте рассмотрим еще один простейший числовой пример. Вам нужно дать стоимостную оценку фиксированного платежа в размере 1 млн дол., который должен быть получен согласно контракту от надежной преуспевающей компании через год. После удержания налога по ставке 35% приток денежных средств составит 650 тыс. дол.
Поскольку контракт порождает эквивалентный долгу денежный поток, альтернативные издержки равны процентной ставке, которую инвесторы потребовали бы от однолетних векселей надежной компании. Предположим, она равна 8%. Для упрощения допустим, что ставка заимствования у вашей фирмы такая же. Следуя нашему принципу оценки эквивалентных долгу денежных потоков, дисконтируем по ставке г* = rD(\ — Тс) = = 0,08(1 – 0,35)= 0,052:
PV = $650 000 / 1.052 = 617 900 дол
Какова кредшпоемкостъ этого платежа в размере 650 тыс. дол.? Ровно 617 900 дол. ~Щ~
Ваша фирма могла бы занять такую сумму и полностью погасить заем — основную сумму долга с процентами в посленалоговом выражении — за счет поступления 650 тыс. дол. Кредитоемкость составляет 100% приведенной стоимости эквивалентного долгу денежного потока.
При таком подходе оказывается, что наша ставка дисконтирования гд(1 — Тс) есть всего лишь особый случай WACC для коэффициента долговой нагрузки 100% (D/V= 1):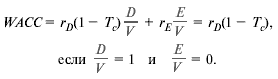
Теперь займемся скорректированной приведенной стоимостью. Расчет APVраспадается на две части. Во-первых, дисконтируем приток 650 тыс. дол. по альтернативным издержкам привлечения капитала 8%. Во-вторых, прибавляем к полученной величине приведенную стоимость процентной налоговой защиты по долгу, поддерживаемому проектом. Коль скоро фирма способна занять 100% стоимости денежного потока, налоговая защита равна rDTcAPV. Тогда APV.
APV = $650 000 / 1.08 + 0.08*0.35*APV / 1.08
После преобразования получаем APV= 617 900 дол. — тот же самый ответ, какой дает нам дисконтирование по посленалоговой ставке заимствования. Стало быть, наша оценка эквивалентного долгу денежного потока есть всего лишь особый случай APV.
СПРАШИВАЕТЕ – ОТВЕЧАЕМ
Вопрос. Из всех этих формул затрат на капитал какую на практике используют финансовые менеджеры?
Ответ. В основном формулу посленалоговых средневзвешенных затрат на капитал. WACC определяются для компаний, иногда для целых отраслей. Мы рекомендуем отраслевые WACC, когда доступны данные по некоторому количеству хорошо сопоставимых фирм. Такие фирмы должны иметь сходные активы, параметры основной деятельности, деловые риски и перспективы роста.
Разумеется, компании-конгломераты, чьи подразделения действуют в нескольких несопряженных отраслях, не могут пользоваться единственным показателем средневзвешенных затрат на капитал, будь то WACC самой компании или WACC одной отрасли. Таким компаниям следует определять отдельные отраслевые WACC для каждого хозяйственного подразделения.
Вопрос. Но WACC служит верной ставкой дисконтирования только для «средних» проектов. А что, если проект существенно отличается схемой финансирования от компании или отрасли?
Ответ. Помните, что инвестиционные проекты не финансируются изолированно. Но даже если так и происходит, нужно смотреть не на то, из каких источников привлекаются деньги непосредственно для проекта, а на то, какой вклад он вносит в общую кредитоемкость фирмы. (Представьте себе, что некий проект удобно финансировать из банковской ссуды. Но это вовсе не означает, что сам по себе проект поддерживает 100% этого долга. Компания занимает деньги и под свои нынешние активы, а не только под проект.)
Но если проект существенно отличается от нынешних активов компании уровнем, кредитоемкости либо если общая политика заимствования компании радикально меняется, в показатель WACC следует внести поправки. Для такой коррекции можно воспользоваться процедурой из трех действий, которая описана в разделе 19.3.
Вопрос. Как вычислить посленалоговые средневзвешенные затраты на капитал с помощью модели оценки долгосрочных активов?
Ответ. Прежде всего введите в формулу оценки долгосрочных активов бету акций, чтобы вычислить г-?, ожидаемую доходность акций. Затем подставьте полученное значение, наряду с величиной посленалоговых затрат на заемный капитал и коэффициентами долг/стоимость и собственный капитал/стоимость, в формулу WACC. В общем, все точно так же, как в главе 9, только с одним отличием: здесь мы используем посленалоговые затраты на заемный капитал, г^(1 — Тс).
Разумеется, модель оценки долгосрочных активов (МОДА) — не единственный способ оценить затраты на собственный капитал. Например, вы могли бы еще воспользоваться моделью арбитражного ценообразования (МАЦ, см. разд. 8.4) или моделью дисконтирования дивидендов (см. разд. 4.3).
Вопрос. Кажется, мне теперь понятно, как учитывать изменения кредитоемкости или политики заимствования. А что делать с изменениями делового риска?
Ответ. Если меняется деловой риск, то меняются и альтернативные издержки привлечения капитала (г).
Найти верное значение г для необычно надежного или, наоборот, рискованного проекта — непростая задача. Иногда финансовые менеджеры могут воспользоваться оценками риска и ожидаемой доходности фирм, сходных с проектом своими характеристиками. Допустим, к примеру, что традиционная фармацевтическая компания обдумывает перспективы масштабных вложений в биотехнологические исследования. Финансовый менеджер мог бы наметить выборку специализированных биотехнологических фирм, оценить их среднюю бету и средние затраты на капитал, а потом принять эти оценки за «эталонные» показатели в сравнительном анализе своего инвестиционного проекта.
Но зачастую бывает трудно найти подходящую выборку сопоставимых компаний для особенно надежных или рискованных проектов. В таких случаях финансовому менеджеру приходится корректировать альтернативные издержки привлечения капитала по собственному усмотрению, исходя из своих знаний и здравых суждений30. В этом ему может пригодиться материал раздела 9.5.
Вопрос. Давайте вернемся к формулам затрат на капитал. Сбивают с толку налоговые ставки. Когда надо использовать Тс, а когда — 7*?
Ответ. Всегда используйте предельную ставку корпоративного налога Тс, когда: (1) рассчитываете WACC как средневзвешенную затрат на заемный и собственный капитал и (2) дисконтируете надежный номинальный денежный поток. В каждом из этих случаев ставка дисконтирования корректируется только на корпоративный налог31.
Что касается APV, то здесь в принципе требуется 7*, чистая налоговая экономия в расчете на доллар выплаченных фирмой процентов по долгу. Эта величина зависит от эффективной ставки личного налога на процентный доход и доход по акциям. 7* почти наверняка меньше 7С, но определить эту разницу количественно очень трудно. В силу этого на практике почти всегда используют 7С как допустимое приближение.
РЕЗЮМЕ
Инвестиционным решениям всегда сопутствуют побочные эффекты, связанные с финансированием: каждый потраченный доллар нужно откуда-то взять. Иногда эти побочные эффекты не имеют значения, по крайней мере существенного. В идеальном мире, где нет налогов, издержек по сделкам и других несовершенств рынка, на стоимость фирмы влияют только инвестиционные решения. В таком мире фирмы могут анализировать инвестиционные возможности так, словно бы финансирование осуществлялось полностью из собственного капитала. Фирма должна решить, какие активы покупать, а затем позаботиться о том, чтобы раздобыть деньги на их оплату. Тому, кто принимает инвестиционные решения, не нужно думать о том, откуда приходят деньги, поскольку политика заимствования, дивидендная политика и все прочие обстоятельства, связанные с выбором источника финансирования, не отражаются на благосостоянии акционеров.
На практике побочные эффекты нельзя игнорировать. Есть два способа их учесть. Вы можете либо вычислить чистую приведенную стоимость дисконтированием по скорректированной ставке, либо сперва дисконтировать по альтернативным издержкам привлечения капитала, а затем прибавить к полученной величине (или вычесть из нее) приведенную стоимость побочных эффектов финансирования. Второй прием называют методом скорректированной приведенной стоимости (APV).
В качестве скорректированной ставки дисконтирования чаще всего используют пос-леналоговые средневзвешенные затраты на капитал (WACC):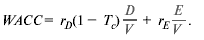
Здесь rj) и Г]? — это показатели ожидаемой доходности, требуемой инвесторами в долговые обязательства и акции фирмы соответственно; DHE— текущие значения рыночной стоимости долга и собственного капитала (акций); V— совокупная рыночная стоимость фирмы (V= D+ Е).Строго говоря, эта формула пригодна только для проектов, которые являют собой
точную копию самой фирмы: проектов с таким же, как и у фирмы, деловым риском, /А,
финансирование которых оставляет неизменным нынешний коэффициент долговой т^
нагрузки фирмы (по рыночной стоимости). Но фирмы могут принять WACC за «эталонную» ставку дисконтирования, при необходимости внося в нее поправки на изменения делового риска или способа финансирования. Мы изложили здесь трехэтапную процедуру коррекции WA С С компании с учетом разницы в коэффициентах долговой нагрузки проекта и самой компании.
Дисконтирование денежного потока проекта по WACC предполагает восстановление определенной пропорции долга в каждый период, так чтобы отношение долга к рыночной стоимости сохранялось постоянным. При этом величина долга, поддерживаемого проектом, должна расти или сокращаться в зависимости от фактических успехов в реализации проекта. Мы назвали это финансовым правилом 2. Кроме того, формула WACC опирается на предпосылку, что способ финансирования имеет значение лишь в связи с процентной налоговой защитой. Когда это или другие условия нарушаются, абсолютно верный ответ дает только метод APV.
В методе APV нет ничего сложного — по крайней мере на уровне понятий. Сначала вычисляется приведенная стоимость проекта в отсутствие каких-либо важных побочных эффектов финансирования. Затем в эту базовую приведенную стоимость вносятся поправки для определения общего воздействия проекта на стоимость фирмы. Как правило, принимать проект следует лишь при условии, что скорректированная приведенная стоимость (APV) имеет положительное значение:
Принимать Проект, еСЛИ APV= базовая NPV+ -Рубочные эффекты
Базовая NPV— это чистая приведенная стоимость проекта, вычисленная при следующих предпосылках: финансирование осуществляется полностью из собственного капитала и рынки капитала совершенны. Представьте себе, что проект выделен в самостоятельную мини-фирму и вам надо определить ее стоимость: вы прогнозируете соответствующий денежный поток и дисконтируете его по альтернативным издержками привлечения кaпитала для проекта. Денежный поток должен быть «очищен» от налогов, которые платила бы мини-фирма, финансируемая целиком из собственного капитала.
Побочные эффекты финансирования оцениваются по одному, и приведенная стоимость каждого прибавляется к (или вычитается из) базовой NPV. Мы рассматривали несколько случаев.
- Эмиссионные издержки. Если принятие проекта понуждает фирму к выпуску ценных бумаг, приведенную стоимость эмиссионных издержек следует вычесть из базовой NPV.
- Процентная налоговая защита. Проценты по долгу — это расходы, подлежащие выче ту из налоговой базы. Большинство людей считает, что процентная налоговая защита увеличивает стоимость фирмы. Стало быть, проект, заставляющий фирму делать боль ше займов, создает добавленную стоимость. Скорректированная приведенная сто имость (APV) проекта возрастает на приведенную стоимость процентной налоговой защиты по долгу, поддерживаемому проектом.
- Особое финансирование. Иногда с принятием проекта связаны особые возможности финансирования. Например, правительства иногда поддерживают социально значи мые проекты предоставлением возвратных субсидий. Просто вычислите приведенную стоимость этой финансовой возможности и прибавьте ее к базовой NPV.
Не следует путать вклад (проекта) в корпоративную кредитоемкость с непосредственным источником финансирования инвестиций. Скажем, фирма может, просто ради удобства, занять 1 млн дол. для вложения в исследовательскую программу. Но едва ли программа увеличивает кредитоемкость фирмы на 1 млн дол.; большая часть из этой суммы нового долга ляжет на другие активы фирмы.
Помните также, что кредитоемкость не означает абсолютный лимит на сумму займов, которую фирма может себе позволить. Это понятие относится к тому, сколько фирма предпочитает занимать. Обычно оптимальный уровень долга фирмы повышается с ростом ее активов; поэтому-то мы и говорим о том, что новый проект увеличивает корпоративную кредитоемкость.
Расчет APV порой требует нескольких действий: по одному на базовую NPV и на каждый из побочных эффектов финансирования. Но многие фирмы стараются вычислять APV «единым махом» посредством следующей процедуры: посленалоговый денежный поток прогнозируется обычным образом (как если бы проект финансировался полностью из собственного капитала), но в ставку дисконтирования вносятся поправки на побочные эффекты финансирования. Если коррекция ставки дисконтирования произведена верно, то итоговая APV такова:
NPV(no скорректированной ставке) = APV= = NPV(no альтернативным издержкам) + PVno6o4aue эффекты-
Преобладающий пример скорректированной ставки дисконтирования — WACC.
Эта глава почти на 100% состоит из теории. Теория сложная. Если вам кажется, что вы с первого раза усвоили все формулы, предпосылки и взаимосвязи, советуем обратиться к психиатру. И все же мы можем предложить вам одно железное правило, простое и легко запоминаемое: дисконтируйте надежный номинальный денежный поток по посленалоговой ставке заимствования.

