ВВЕДЕНИЕ
етод дисконтированных денежных потоков (DCF) был разработан в 1930-е гг. Автором данного метода считается выдающийся экономист И. Фишер, который в работе «Теория процентных ставок» (1930 г.) ввел понятие чистой приведенной стоимости (NPV) [2]. В дальнейшем значительный вклад в развитие метода внесли такие экономисты, как Д. Кейнс (предложил концепцию внутренней ставки доходности – IRR) и Э. Соломон [6], который разработал идею остаточной, или конечной, стоимости (Terminal Value) компании. Вот уже более 70 лет DCF является одним из основных инструментов финансовых аналитиков: он в различных вариантах широко
используется для оценки фундаментальной стоимости компаний и вычисления чистой приведенной стоимости инвестиционных проектов.
Несмотря на свою популярность, данный метод имеет ряд широко известных недостатков как с теоретической, так и с практической точки зрения. На практическом уровне метод дисконтированных денежных потоков является очень чувствительным к изменениям в параметрах финансовой модели – например, в ставке дисконтирования или темпах роста денежных потоков. В результате небольшие изменения в этих параметрах могут привести к существенным колебаниям чистой приведенной стоимости проектов и / или фундаментальной стоимости компаний.
На теоретическом уровне метод дисконтированных денежных потоков не учитывает вероятностный характер результатов инвестиционного проекта, игнорирует стратегическую составляющую стоимости компаний и не позволяет оценить вклад в стоимость управленческой гибкости (т. е. возможности принимать
оптимизирующие управленческие решения по ходу реализации проектов). Особенно плохо работает DCF в условиях высокой неопределенности и риска.
За последние 20 лет были разработаны многочисленные альтернативные методы, частично устраняющие недостатки метода DCF. На рис. 1. показана классификация существующих методов оценки стоимости и инвестиционной привлекательности в зависимости от наличия стратегических и рыночных рисков.
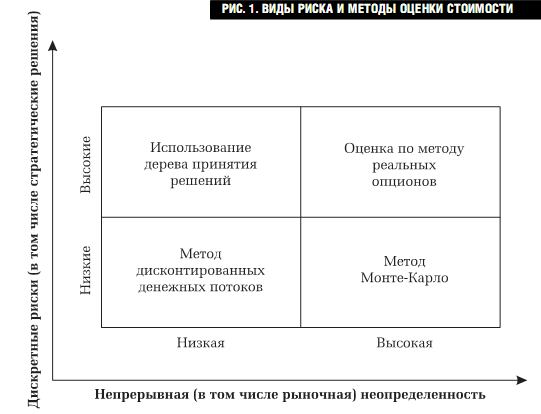
Все виды риска можно условно разделить на две основные категории: дискретные риски и непрерывные риски (непрерывная неопределенность). К дискретным можно отнести риски, связанные со стратегическими решениями, к непрерывным же относятся рыночные риски, или риски колебания рыночных факторов (цена, процентные ставки, обменные курсы и т. д.).
Метод дисконтированных денежных потоков дает удовлетворительные результаты, только если дискретные и непрерывные риски находятся на низком уровне. В случае наличия
значительных дискретных рисков используется метод дерева решений. При значительной непрерывной неопределенности применяется компьютерное моделирование по методу Монте-Карло. Наконец, при наличии высокого уровня непрерывной неопределенности и значительных дискретных рисков применяется метод реальных опционов1. Следует отметить, что на различных этапах жизненного цикла компании / проекта на первый план могут выдвигаться либо дискретные, либо непрерывные риски. На начальных этапах (например, на этапе разработки нового продукта) значительную роль играют дискретные риски, а на поздних этапах (например, на этапе коммерциализации и продаж) – непрерывные рыночные риски.
Существует значительное количество теоретической и аналитической литературы по данной проблеме. В этой статье мы на четырех конкретных практических примерах продемонстрируем применение метода Монте-Карло для анализа инвестиционных проектов и расчета фундаментальной стоимости акций
в условиях высокого уровня непрерывной неопределенности.
ПРИМЕНЕНИЕ МЕТОДА МОНТЕ-КАРЛО ПРИ АНАЛИЗЕ ПРИВЛЕКАТЕЛЬНОСТИ ИНВЕСТИЦИОННОГО ПРОЕКТА
В данном разделе мы рассмотрим применение метода Монте-Карло для анализа привлекательности весьма простого инвестиционного проекта.
Описание проекта: фармацевтическая компания рассматривает вопрос о приобретении для последующего производства патента нового лекарственного препарата. Лекарство примечательно тем, что не имеет побочных эффектов. Стоимость патента составляет $3,4 млн.
Необходимо подготовить финансовый анализ приобретения данного патента методом дисконтированных денежных потоков, рассчитать NPV и IRR проекта. Горизонт расчетов составляет три года. Стандартная финансовая модель приводится на рис. 2. Согласно прогнозам аналитиков, компания в первый, второй и третий год проекта продаст соответственно 802 тыс., 967 тыс. и 1132 тыс. упаковок лекарства по цене $6, $6,05 и $6,10 за упаковку.
| Год 0 | Год 1 | Год 2 | Год 3 | |
| Цена упаковки | $6,00 | $6,05 | $6,10 | |
| Количество проданных, шт. | 802000 | 967000 | 1132000 | |
| Выручка | $4 812 000 | $5 850 350 | $6 905 200 | |
| Себестоимость | $2 646 600 | $3 217 693 | $3 797 860 | |
| Валовая прибыль | $2 165 400 | $2 632 658 | $3 107 340 | |
| Операционные издержки | $324 810 | $394 899 | $466 101 | |
| Чистый доход до налогов | $1 840 590 | $2 237 759 | $2 641 239 | |
| Налоги | $588 989 | $716 083 | $845 196 | |
| Стартовые инвестиции | -$3 400 000 | |||
| Чистый доход | -$3 400 000 | $1 251 601 | $1 521 676 | $1 796 043 |
| NPV (3 года) | $344 796 | |||
| IRR (3 года) | 15% |
Ставка налога на прибыль равна 32%, ставка дисконтирования равна 10%, себестоимость составляет 55%, а операционные издержки – 15% от цены препарата. Для вычисления NPV и IRR проекта в Excel использовались функции ЧПС («Чистая приведенная стоимость») и ВСД («Внутренняя ставка доходности»). По результатам расчетов IRR проекта составляет 15%, а NPV – $344,8 тыс. Поскольку NPV > 0, то компании следует принять проект.
Несмотря на положительные результаты стандартного анализа все равно в полученных прогнозах нельзя быть полностью уверенными. Рынок лекарственных препаратов является весьма конкурентным. Конкуренция со стороны других препаратов может привести к снижению цены ниже прогнозируемой. Также из-за влияния конкуренции трудно точно предсказать объем продаж препарата (количество упаковок). Помимо цены и объема продаж не поддаются точному прогнозу будущая себестоимость препарата и операционные издержки. Очень часто себестоимость и издержки превышают запланированные. Кроме того, они могут колебаться год от года.
В данном случае мы имеем дело с высоким уровнем непрерывной (рыночной) неопределенности, поэтому стандартная финансовая модель по методу DCF не может дать достаточных для принятия решения результатов. Для одновременного учета неопределенности в цене, продажах, себестоимости и издержках применяется анализ по методу Монте-Карло. Основные параметры финансовой модели – цена, объем продаж – моделируются как случайные переменные, имеющие вероятностное распределение. Анализ по методу Монте-Карло предоставит необходимую информацию для ведения более обоснованных переговоров о покупке патента на изготовление лекарства, а также позволит понять, какие факторы в
наибольшей степени повлияют на финансовые результаты проекта.
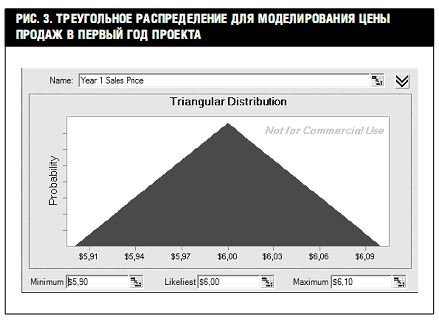
Для моделирования цены продажи (в первый, второй и третий год проекта отдельно) используется треугольное распределение. Треугольное распределение имеет три параметра – минимальное значение, максимальное значение и наиболее вероятное значение. Его, как правило, используют для моделирования параметров, которые менеджеры в значительной степени могут контролировать. Цена продажи в первый год имеет минимальное значение $5,90, максимальное значение – $6,10 и наиболее вероятное значение – $6,00 (рис. 3). Аналогично, цена продажи во второй год имеет треугольное распределение с параметрами $5,95; $6,05; $6,15. Цена продажи на третий год имеет треугольное распределение с параметрами $6,00; $6,10; $6,20.
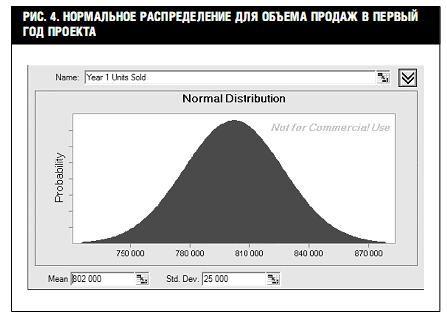
В отличие от цены, которая колеблется, но находится по контролем менеджеров компании, объем продаж зависит от не контролируемых фирмой факторов. Как правило, объем продаж моделируется как случайная переменная с нормальным распределением.
Объем продаж в первый год имеет нормальное распределение со средним значением (математическим ожиданием) $802 тыс. и стандартным отклонением $25 тыс. (рис. 4). Аналогично, объем продаж во второй год имеет нормальное распределение с ожиданием $967 тыс. и стандартным отклонением $30 тыс. Наконец, объем продаж в третий год имеет нормальное распределение с ожиданием $1132 тыс. и стандартным отклонением $25 тыс.
Себестоимость (процент от продаж), как предполагается, имеет треугольное распределение с минимальным значением 50%, максимальным значением 65% и наиболее вероятным значением 55%. Следует отметить, что в данном случае треугольное распределение имеет не симметричную форму, а немного скошено вправо, т. е. имеется большая вероятность того, что себестоимость будет завышена, а не занижена по сравнению с наиболее вероятным значением. Операционные издержки (процент от продаж) моделируются как нормальное распределение с ожиданием 15% и стандартным отклонением 2%.
Всего в ходе анализа по методу Монте-Карло было сделано 10 тыс. повторов. При каждом повторе программа генерировала новые
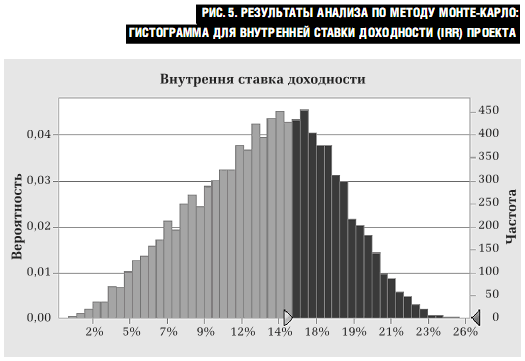
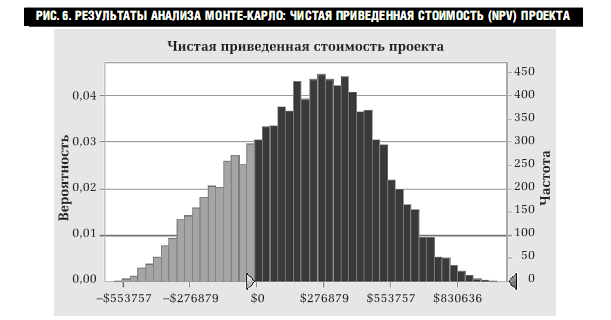
значения для случайных переменных (параметров финансовой модели) и вычисляла значение NPV и IRR проекта. Результаты анализа в виде гистограммы показаны на рис. 5 и рис. 6. и обобщены в табл. 1.
| Среднее | Минимум | Максимум | P10 | P50 | P90 | ||||||||
| IRR, % | 13 | 0 | 26 | 7 | 13 | 19 | |||||||
| NPV, $ | 202,3 тыс. | –637,9 тыс. | 1044 тыс. | –189,8 тыс. | 221,5 тыс. | 560 тыс. |
Как видно из табл. 1, средняя NPV проекта составляет 202 тыс., что значительно меньше, чем NPV стандартной модели (344,8 тыс.) Это результат скошенного вправо распределения себестоимости. Анализ по методу Монте-Карло показывает: вероятность того, что NPV проекта будет положительной, не является стопроцентной. Как видно из гистограммы, существует вероятность (почти 25%) того, что NPV проекта окажется отрицательным. Таким образом в одной четвертой всех случаев при определенной комбинации факторов компания понесет потери. В то же время при благоприятном стечении факторов NPV проекта может превышать $1 млн.
МЕТОД МОНТЕ-КАРЛО И ОПТИМИЗАЦИЯ. ВЫЧИСЛЕНИЕ И ОПТИМИЗАЦИЯ NPV ПРОЕКТА ПО РАЗРАБОТКЕ НЕФТЯНОГО МЕСТОРОЖДЕНИЯ
Анализ Монте-Карло можно использовать не только для более реалистичной оценки инвестиционной привлекательности проекта, но также и для выбора оптимальной комбинации параметров проекта. Рассмотрим проект по разработке нефтяного месторождения. В основе модели проекта лежат предварительные данные о величине резервов2 месторождения3. Задача анализа – основываясь на величине запасов и проценте нефтеотдачи (Recovery Rate),
рассчитать NPV проекта, а также определить оптимальные темпы добычи нефти и оптимальное количество скважин на месторождении.
В качестве критерия оптимизации выбран десятый процентиль распределения NPV проекта – нефтяная компания хочет максимизировать такое значение NPV, которого она может
достигнуть или превысить с 90%-ной вероятностью.
График добычи нефти включает три этапа:
- фаза роста добычи – период введения в работу новых скважин;
- фаза плато: после достижения определенного уровня добычи (плато), добыча продолжается на постоянном уровне до тех пор, пока пластовое давление остается постоянным и пока не добыта определенная доля резервов;
- фаза снижения добычи – период, когда темпы добычи равномерно снижаются с течением времени. Темпы добычи на этом этапе описываются с помощью экспоненциальной функции:
P(t) = P(0) exp(-ct),
где t – время после начала фазы плато, а c – константа.
Первичные данные для анализа представлены в табл. 2 и табл. 3.
Дополнительные вычисления для анализа представлены в табл. 4.
Годовая добыча вычисляется отдельно для трех фаз развития проекта:
в фазе плато: годовая добыча

