Как грамотно моделировать и измерять риски
МЕТОД МОНТЕ-КАРЛО ПОЗВОЛЯЕТ ПРОГНОЗИРОВАТЬ НЕ ТОЛЬКО ЦЕНУ АКЦИЙ. С ЕГО ПОМОЩЬЮ МОЖНО МОДЕЛИРОВАТЬ ИНВЕСТИЦИОННЫЕ ПРОЕКТЫ, А ТАКЖЕ ОБЪЕМЫ И ЭФФЕКТИВНОСТЬ ПРОДАЖ.
Для измерения и моделирования рисков, возникающих при работе на финансовом рынке, сегодня широко используются стохастические (вероятностные) методы, в том числе метод Монте-Карло. Однако инвестиционные аналитики как будто не замечают этих эффективных инструментов и продолжают строить свои точечные детерминистические прогнозы на основе одной из многочисленных разновидностей метода дисконтированных денежных потоков.
70 лет одиночества
Метод дисконтированных денежных потоков (Discounted Cash Flow) был разработан в 30-е годы прошлого столетия и вот уже более семидесяти лет используется для определения фунда –
ментальной стоимости компаний и цены акций. Несмотря на свою популярность, DCF имеет ряд широко известных недостатков, которые касаются как теории, так и практики его применения. На практическом уровне метод дисконтированных денежных потоков является очень чувствительным к изменениям в параметрах финансовой модели, например, к ставке дисконтирования или темпам роста денежных потоков. В результате небольшие изменения в параметрах могут привести к существенным колебаниям чистой приведенной стоимости проектов и/или фундаментальной стоимости компаний. В теоретическом плане метод дисконтированных денежных потоков не учитывает вероятностный характер результатов инвестиционного проекта, а кроме того, игнорирует стратегическую составляющую стоимости компаний.

Рис. 1 Виды риска и методы оценки стоимости
Не принимается в расчет и управленческий вклад в стоимость – возможность принятия менеджментом оптимизирующих решений по ходу реализации проектов. Особенно плохо работает DCF в условиях высокой неопределенности и риска. За последние двадцать лет были разработаны многочисленные альтернативные методы, частично устраняющие недостатки DCF. На рис. 1 показана классификация существующих методов оценки стоимости инвестиционной привлекательности в зависимости от наличия стратегических и рыночных рисков. Все виды риска можно условно разделить на две основные категории: дискретные и непрерывные (непрерывная неопределенность). К дискретным рискам можно отнести угрозы, связанные со стратегическими решениями. Непрерывные риски включают рыночные риски, или риски колебания рыночных факторов (цена, процентные ставки, обменные курсы и т.д.).
Причем метод Монте-Карло подходит не только для прогнозирования цены акций – его можно применить для оценки инвестиционных проектов или для планирования эффективности продаж. Иными словами, это универсальный инструмент с множеством функций. На примерах мы рассмотрим лишь некоторые из них.
Выбор оружия
Метод дисконтированных денежных потоков дает удовлетворительные результаты, только если дис кретные и непрерывные риски находятся на низком уровне. Когда возникают значительные дискретные риски, используется метод дерева решений. Если же на первый план выходит непрерывная неопределенность, применяется компьютерное моделирование по методу Монте-Карло. В тех случаях, когда значительны оба вида рисков – дискретные и непрерывные, применяется метод реальных опционов. Следует отметить, что на различных стадиях жизненного цикла компании/проекта угрозы проявляются по-разному. На начальных этапах (например, разработка нового продукта, строительство новых мощностей) более значительную роль играют дискретные риски, а на последующих (этап коммерциализации и продаж) – непрерывные рыночные риски.
таблица 1 ФИНАНСОВАЯ МОДЕЛЬ ДЛЯ ПРОЕКТА ПО ПОКУПКЕ ПАТЕНТА НА ИЗГОТОВЛЕНИЕ ПРЕПАРАТА
| ГОД 0 | ГОД 1 | ГОД 2 | ГОД 3 | |
| Цена упаковки, $ | 6.0 | 6.05 | 6.10 | |
| Кол-во проданных, шт. | 802000 | 967000 | 1132000 | |
| Выручка,$ | 4812000 | 5850350 | 6905200 | |
| Себестоимость, $ | 2646600 | 3217693 | 3797860 | |
| Валовая прибыль, $ | 2165400 | 2632658 | 3107340 | |
| Операционные издержки, $ | 324810 | 394899 | 456101 | |
| Чистый доход до налогов, $ | 1840590 | 2237759 | 2541239 | |
| Налоги, $ | 588989 | 715083 | 845196 | |
| Стартовые инвестиции, $ | -3400000 | 715083 | 845196 | |
| Чистый доход, $ | -3400000 | 1251601 | 1521676 | 1796043 |
| NPV(3 года), $ | 344796 | |||
| IRR(3 года), $ | 15 |
В ценовом треугольнике
Фармацевтическая компания изучает вопрос о приобретении патента на производство нового лекарственного препарата. Стоимость патента составляет $3 400 тыс. Необходимо подготовить финансовый анализ приобретения этого лекарства методом дисконтированных денежных потоков, посчитать NPV проекта. Горизонт расчетов составляет три года. Стандартная финансовая модель приводится в табл. 1. Согласно прогнозам аналитиков компания в первый, второй и третий годы проекта продаст 802 тыс., 967 тыс. и 1132 тыс. упаковок лекарства по цене $6, $6,05 и $6,1 за упаковку соответственно. Ставка налога на прибыль равна 32%, ставка дисконтирования – 10%, себестоимость составляет 55%, а операционные издержки – 15% от цены препарата. Для вычисления NPV и IRR проекта в Excel использовались функции ЧПС (чистая приведенная стоимость) и ВСД (внутренняя ставка доходности, IRR).
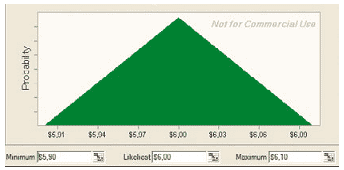
Рис. 2. Треугольное распределение для моделирования цены продаж в первый год проекта 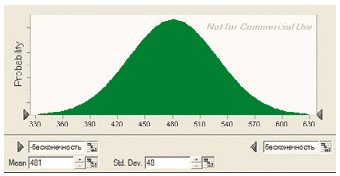
Рис. 3. Нормальное распределение для объема продаж в первый год проекта
По результатам расчетов IRR проекта равен 15%, а NPV – $344,8 тыс. Поскольку полученный показатель NPV больше 0, компании следует принять проект. Однако несмотря на положительные результаты стандартного анализа, остаются некоторые сомнения относительно точности полученных прогнозов. Конкуренция на фармацевтическом рынке достаточно жесткая, возможно ценовое давление со стороны других производителей аналогичных медикаментов. Это может привести к снижению цены ниже прогнозируемой, а также к изменению предполагаемого объема продаж. Помимо цены и объема продаж не поддается точному прогнозу будущая себестоимость пре –
парата и операционные издержки – нередко эти показатели превышают запланированные значения. Кроме того, они могут колебаться из года в год.
В данном случае мы имеем дело с высоким уровнем непрерывной (рыночной) неопределенности. Поэтому стандартная финансовая модель, выстроенная по методу DCF, не может дать результатов, на основе которых можно было бы принять однозначное решение – приобретать патент или нет. Для одновременного учета неопределенности в цене, продажах, себестоимости и издержках подходит анализ по методу Монте-Карло. Основные параметры финансовой модели – цена, объем продаж – моделируются как случайные переменные, имеющие вероятностное распределение. Анализ Монте-Карло предоставит необходимую информацию для ведения более обоснованных переговоров о покупке патента на изготовление лекарства, а также позволит понять, какие факторы в наибольшей степени влияют на финансовые результаты проекта. Для моделирования цены продажи (в первый, второй и третий годы проекта отдельно) используется треугольное распределение: между минимальным и максимальным находится наиболее вероятное значение выбранного параметра. Такое распределение, как правило, используется для моделирования параметров, в значительной
Рис. 2. Треугольное распределение для моделирования цены продаж в первый год проекта
Рис. 3. Нормальное распределение для объема продаж в первый год проекта
степени контролируемых менеджерами проекта. Цена продажи в первый год (рис. 2) имеет минимальное значение $5,90, максимальное – $6,10 и наиболее вероятное значение $6,00. Аналогично цена продажи для второго года имеет треугольное распределение с параметрами $5,95, $6,05 и $6,15. Цена продажи в третий год имеет треугольное распределение с параметрами $6,00, $6,10 и $6,20.
В отличие от цены, которая хотя и колеблется, но находится под контролем менеджеров компании, объем продаж зависит от неконтролируемых фирмой факторов. Как правило, объем продаж моделируется как случайная переменная с нормальным распределением.
Объем продаж в первый год (рис. 3) имеет нормальное распределение со средним значением (математическим ожиданием) 802 тыс. упаковок и стандартным отклонением 25 тыс. упаковок. Для второго и третьего года были получены следующие пары значений «ожидание / отклонение»: 967 тыс./30 тыс. и 1132 тыс./25 тыс. упаковок соответственно.
Себестоимость (как процент от продаж) имеет треугольное распределение с минимальным значением 50%, максимальным значением 65% и наиболее вероятным значением 55%. Следует отметить, что в данном случае треугольное распределение имеет не симметричную форму, а немного скошено вправо – себестоимость скорее будет завышена, чем занижена по сравнению с наиболее вероятным значением. Операционные издержки (процент от продаж) моделируется как нормальное распределение с ожиданием 15% и стандартным отклонением 2%. Всего в ходе анализа Монте-Карло было сделано 10 тыс. повторов. При каждом повторе программа генерирует новые значения для случайных переменных (параметров финансовой модели) и вычисляет значение NPV проекта. Результаты анализа в виде гистограммы показаны на рис. 4 и обобщены в табл. 2.
Как видно из табл. 2, среднее значение NPV проекта составило всего $202 тыс., что значительно меньше результата ($344,8 тыс.), полученного стандартным методом дисконтированных потоков. Это расхождение – результат скошенного вправо распределения себестоимости. Кроме того, анализ по методу Монте-Карло показывает, что вероятность получения положительного NPV проекта далека от 100%. Как видно из гистограммы, почти в 25% случаев прогнозируемый NPV проекта оказался отрицательным. В то же время при благоприятном стечении факторов NPV проекта может превышать $1 млн.
Точная калибровка
В приведенном выше примере для моделирования продаж было выбрано нормальное распределение. Однако в случае, если имеются исторические данные, рекомендуется использовать их для калибровки распределения, которое описывает параметры финансовой модели. Предположим, требуется спрогнозировать валовую прибыль продаж двух продуктов, используя простую финансовую модель (см. табл. 3).
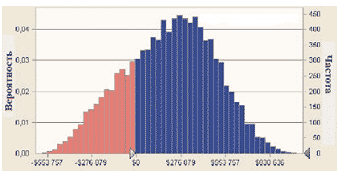
Рис. 4.Результаты анализа Монте-Карло: распределение NPV проекта
Однако на этот раз у нас есть исторические данные о продажах этих продуктов в течение 360 предыдущих периодов (рис. 5). В этом случае мы можем на основе имеющихся данных проверить, какое распределение лучше всего подходит для прогноза продаж.
Используя, как и в первом примере, программу Crystal Ball, удалось подобрать распределение, которое наиболее точно со статистической точки зрения подходит для моделирования продаж продукта (1): это лог-нормальное распределение с ожиданием 499 и стандартным отклонением 176 (рис. 6). Для продукта (2) лучше всего подходит нормальное распределение с ожиданием 481 и отклонением 48 (рис. 7).
Используя подобранные распределения, получаем прогноз совокупной валовой маржи продаж двух продуктов (рис. 8).
Непредсказуемое IPO
Давайте посмотрим на метод Монте-Карло в ситуации, когда требуется спрогнозировать цену акций компании. Задача – оценить стоимость компании Netscape Communication Corporation. Эта финансовая модель была разработана андеррайтерами компании при выходе Netscape на IPO. Размещение состоялось 9 августа 1995 года, а Netscape стала первой публичной интернет-компанией.
Андеррайтеры компании планировали предложить к размещению 5 млн акций допэмиссии по цене $28 за каждую. До этого на венчурном этапе в Netscape было инвестировано только $27 млн, и к моменту выхода на IPO компания еще была убыточна. Балансовая стоимость компании составляла $16 млн. При цене размещения $28 за акцию рыночная капитализация Netscape должна была превысить $1 млрд.
таблица 2 РЕЗУЛЬТАТЫ АНАЛИЗА МОНТЕ-КАРЛО ДЛЯ NPV ПРОЕКТА
| СРЕДНЕЕ | МИНИМУМ | МАКСИМУМ | Р10 | Р50 | Р90 | |
| NPV | 202.3 тыс. | -637.9тыс. | 1044тыс. | -189.8тыс. | 221.5тыс. | 550тыс. |
таблица 3 ПРОСТАЯ МОДЕЛЬ ПРОДАЖ ПРОДУКТОВ
| продукт 1 | продукт2 | |
| Продажи, шт. | 552 | 508 |
| Цена, $ | 4,95 | 5,95 |
| Себестоимость, $ | 2,20 | 2,40 |
| Валовая прибыль, $ | 1546 | 1805 |
| Совокупная валовая прибыль, $ | 3350 |
таблица 4 ОСНОВНЫЕ ПАРАМЕТРЫ И РЕЗУЛЬТАТЫ МОДЕЛИ ОЦЕНКИ СТОИМОСТИ NETSCAPE COMMUNICATION CORPORATION
| Выручка | Рост 65% в год |
| Операционные издержки | 10.4% от выручки |
| Затраты на НИОКР | 35.8% от выручки |
| Амортизация | 5.5% выручки |
| Другие операционные издержки | Процент от выручки: сначала 80% затем убывание до 20% |
| Прибыль до налогов | Выручка – операционные издержки – затраты на НИОКР – амортизация – другие издержки |
| Налоги | Прибыль до налогов x 0,34 |
| Чистый доход | Прибыль до налогов – налоги |
| Капиталовложения | Процент от выручки: сначала от 45% затем убывание до 10% |

