Оценка риска портфельного инвестора

Основной задачей в процессе формирования портфеля ценных бумаг является распределение инвестиций по различным альтернативным вложениям, которые отвечали бы критериям эффективности и оптимальности.

При этом под эффективным портфелем понимается портфель, обеспечивающий требуемый уровень доходности при заданном уровне риска, а под оптимальным портфелем — наиболее предпочтительный из набора эффективных портфелей, обеспечивающий максимальный уровень доходности при заданном уровне риска.

В общем случае доходность актива имеет две составляющие: доход, получаемый за период, и приращение рыночной стоимости данного актива за этот же период.

Риск — это категория неопределенности (в данном случае — неопределенности в получении доходов инвестором), вызывающая у каждого инвестора субъективное отношение к процессу инвестирования, как правило — отношение неприятия риска.

При выборе портфеля инвестиций необходимо решить как минимум две первостепенные задачи — найти доходность каждого конкретного портфеля ценных бумаг и определить его уровень риска. Эти задачи решаются статистическими методами на основе теории Марковица.
Согласно данной методике ожидаемая доходность актива представляется случайной величиной, а риск — мерой неопределенности этой случайной величины.

При этом ожидаемая доходность рискового i-го актива вычисляется как математическое ожидание возможных значений доходности i-го актива: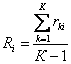
, где

Ri— ожидаемая доходность i-го актива в портфеле за определенный период;
rki — k-е возможное значение доходности i-го актива.

Мерой неопределенности (риска) служит дисперсия возможных значений доходности i-го актива Di, определяемая по формуле: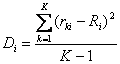

Производными величинами дисперсии являются вариация и среднеквадратическое отклонение. Вариация доходности представляет собой нормированную дисперсию и соотносится с последней как:

Соразмерной с доходностью величиной риска является среднеквадратическое отклонение:

Таким образом, мерой доходности каждого конкретного актива служит математическое ожидание возможных значений доходности этого актива, а мерой риска — дисперсия (вариация или же среднеквадратическое отклонение) возможных значений его доходности.
Как рассчитывается доходность и риск портфеля инвестиций?
Доходность портфеля находится достаточно просто (она определяется как сумма доходностей каждого из активов, взвешенная размерами этих активов):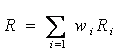
, где

R — доходность портфеля за определенный период;
wi— вес актива в портфеле (его рыночная стоимость на начало периода);
Ri — ожидаемая доходность i-го актива в портфеле за определенный период.

Неопределенность (риск) портфеля определяется через корреляцию Кij:

Коэффициент корреляции — статистический показатель, определяющий степень связи, существующей между двумя случайными величинами, в данном случае — между доходностями двух активов. Положительная корреляция свидетельствует о том, что в среднем изменение этих двух переменных происходит в одном направлении, а отрицательная — в противоположных. Нормированный среднеквадратическими отклонениями доходности коэффициент корреляции представляет собой ковариацию двух случайных величин доходности:
, где

KVin — коэффициент ковариации двух активов;
Kin — коэффициент корреляции этих активов.

Риск портфеля из двух активов рассчитывается по формуле:

,

А риск портфеля, состоящего из I активов:

Таким образом, рискованность (вариация) портфеля активов зависит не только от рискованности (вариации) отдельных активов, но и от ковариаций попарных их комбинаций. Если доходности активов в портфеле мало коррелированны, результирующая вариация портфеля будет ниже, а если они отрицательно коррелированны, вариация портфеля будет минимальна.

В этом и состоит главное содержание принципа диверсификации — в том, чтобы распределить риск среди множества некоррелированных по доходности инвестиций, в результате чего совокупный риск портфеля уменьшится.
Проиллюстрируем изложенное на примере. Пусть три актива А, В и С приносят доход в конце периода на протяжении 12 периодов.

Промежуточные этапы расчетов показаны в таблицах:

Как видно, наименее рискованным портфелем, обеспечивающим приемлемую доходность, является портфель, состоящий из инвестиций А и В (коэффициент ковариации этих активов отрицателен и составляет -0,44).