Портфельные риски в теории Марковица

Портфельные риски в теории Марковица.

Возможно, Вы не знали, что доходы, которые можно получить при портфельном управление в несколько раз превышают банковские проценты, а риски – при взвешенном просчитанном подходе – практически на том же уровне. Это в полном смысле «золотое дно» только начинает разрабатываться в нашей стране, хотя уже давно изучено в Европе и Америке. С уверенностью можно предсказать в ближайшие годы взрыв активности страховых и инвестиционных компаний, пенсионных фондов и банков в данной области.

Читатель, наверное, уже где-то слышало об инвестиционных портфелях. Если так, то это статья расширит Ваши представления об этом финансовом инструменте.

Важное место в технологии портфельного инвестирования занимают статистические методы. На практике математические модели редко применяются для работы с российскими акциями. Причиной тому является низкая эффективность использования математического аппарата в условиях нестабильности. Однако, с постепенной нормализацией политической и экономической ситуации в России актуальность портфельного инвестирования на основе статистических методов будет возрастать. И это уже сейчас происходит.

Среди математических моделей выделяют модели, решающие задачи оптимального формирования портфеля и прогнозирования. Вместе мы рассмотрим методологию построения оптимизационной модели на основе теории Марковица.

Во второй половине двадцатого века господствовала идея о том, что портфель созданный из рисковых активов априори имеет высокий риск. В 1959 г. Марковицем была предложена математическая схема выбора оптимальных портфелей, концентрирующая внимание на поведении портфеля, а не его составляющих. Она коренным образом изменила точку зрения на инвестиционный процесс.

Основной задачей в процессе оптимального формирования портфеля ценных бумаг, является распределение инвестором определенной суммы денег по различным альтернативным вложениям. В общем случае задача оптимизации портфеля состоит в выборе такого распределения средств между активами, при котором происходит максимизация прибыли при заданных ограничениях на уровень риска.

Читатель в этой статье встретит слова «эффективный» и «оптимальный» портфели. Под эффективным понимается портфель, удовлетворяющий требованиям минимального риска и максимального дохода. Если инвестор стоит перед выбором одного из эффективных портфелей, то оптимальным портфелем будет наиболее предпочтительный из них. Предпочтения инвестора – это отношения к риску и ожидаемой доходности вложений. Инвестору часто приходится сталкиваться с выбором рисковых активов, т.е. активов доходность которых в будущем не определена. Кстати, как показывает практика риск актива обратно пропорционален его доходности.

Теперь мы готовы рассмотреть, как измеряется ожидаемая доходность и риск активов, а также ожидаемая доходность портфеля, состоящего из рисковых активов.

Формула доходности инвестиционного портфеля имеет вид:

где Rр – доходность портфеля р за период;

Rg – доходность актива g за период;

wg – вес актива g в портфеле (т.е. доля рыночной тоимости актива g в общей рыночной стоимости всего портфеля);

G – число активов в портфеле.

Пример 1

Пусть инвестиционный портфель состоит из акций ЛУКОЙЛа (20%), Сбербанк (40%) и Мосэнерго (40%) при соответствующей недельной доходности 0,93%, 1,81% и 1,6%. Тогда недельная доходность портфеля будет равна Rр = 0,2*0,93+0,4*1,81+0,4*1,6= 1,55%

Представленная выше формула показывает, что доходность портфеля, состоящего из G активов (Rp), равна сумме всех взвешенных доходностей отдельных активов, входящих в портфель.

Для удачно ведения портфеля, инвестору важно знать его ожидаемую доходность. Ожидаемая доходность портфеля – это взвешенная сумма ожидаемых доходностей активов, входящих в портфель. При этом вес ожидаемой доходности каждого актива определяется как доля рыночной стоимости отдельного актива в общей рыночной стоимости портфеля.

Ожидаемая доходность рискового актива вычисляется следующим образом. Сначала задается распределение вероятностей для возможных значений реализованной доходности. Распределение вероятностей – это функция, сопоставляющая каждое возможное значение доходности и вероятности его реализации. При заданном распределении вероятности ожидаемое значение случайной величины есть взвешенное среднее ее возможных значений, причем роль весов играет вероятность реализации этих значений. Математически ожидаемая доходность актива выражается следующим образом:

где r_n – n-е возможное значение доходности i-го актива;
р_n – вероятность реализации значения доходности п для i-го актива;
N – число возможных значений доходности.

Пример 2

Пусть проведено 100 измерений доходности акции Мосэнерго-3 в 20 случаях она составила 3,5%, в 15 – 2,6% и в 65 случаях была 1%. Тогда математическое ожидание доходности по акции Мосэнерго-3 буде Е(Ri)=3,5*0,2+2,6*0,15+0,65*1=1,74%.

В толковых словарях риск определяется как «подверженность опасности, убыткам, потерям и т.п.». В инвестиционной деятельности понятие риска трансформировалось и стало определяться как вариация или дисперсия доходности актива (меры возможных отклонений от среднего значения). В результате риск получил количественное значение. Заслуга в этом принадлежит Марковицу, который на основе статистического понятия риска создал свою двухпараметрическую модель инвестиционного портфеля.

Формула для определения вариации доходности n-го актива записывается следующим образом:

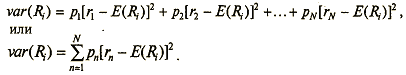
Пример 3

Найдем риск получения средней доходности 1,74% за неделю по акции Мосэнерго-3. Для этого рассчитаем вариацию доходности var(Ri)=0,2*(3,5-1,74)2+0,15*(2,6-1,74)2+0,65*(1-1,74)2=1,0864.

Вариация учитывает не только размер отклонений возможных значений доходности от среднего, но и вероятность такого отклонения, т.е. она указывает меру неопределенности в ожиданиях инвестора, который оценивает будущую доходность как среднюю по всем возможным значениям. Это обстоятельство и позволило Марковицу считать дисперсию доходности мерой риска инвестиций.

Вариация имеет размерность квадрата измеряемой величины, для удобства ее преобразовывают в стандартное отклонение, путем извлечения квадратного корня. В результате получается величина, имеющая ту же размерность, что и доходность

Кстати, наш фондовый рынок еще не достаточно развит и поэтому использование статистических методов имеет свои ограничения. В частности, на ММВБ, на конец 1 квартал 2002 года, существовало всего 17 акций с историческими данными глубиной более двух лет. Иначе говоря, найти ожидаемую доходность и риск с большей долей достоверности можно только на семнадцати акциях из 54 активно торгуемых на ММВБ. Если не учитывать облигации, то узость возможного применения теории Марковица станет еще более очевидна. Выход из данной ситуации использование данных с РТС, но они имеют тоже свои ограничения, связанные с нерегулярностью проходящих сделок. На рисунке 1 представлен график доходности и риска по 16 акциям с достаточными историческими данными. На нем не уместилась привилегированная акция Самарэнерго второго выпуска из-за высокой недельной доходности за двухлетний период.

Рис. 1. Взаимосвязь недельной доходности и риска 16 акций по данным за 2 года

Как было указано выше формула определения вариации дает вариацию отдельного актива. Найти вариацию портфеля из двух активов не намного сложнее. Она зависит не только от вариации двух активов, но и от «степени согласованности» в поведении доходностей активов.

Уравнение имеет вид:

где cov(R_i R_j) – ковариация доходностей активов i и j.

Смысл выше указанного уравнения состоит в том, что вариация доходности портфеля равна взвешенной сумме взвешенных вариаций доходностей двух активов и их ковариации.

Понятие ковариации еще не встречалось в наших обсуждениях. Это – математический термин. В данном контексте он означает степень взаимосвязи доходностей двух активов. Для измерения ковариации нет таких специальных единиц, как, например, доллары или проценты. Положительная ковариация означает, что доходности обоих активов изменяются (в среднем) в одном направлении, а отрицательная – в противоположном. Ковариация двух активов рассчитывается при помощи следующей формулы: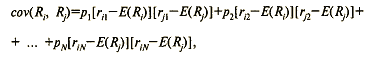

где r_in – n-е возможное значение доходности актива i;

r_jn – п-e возможное доходности актива j;

p_n – вероятность реализации n-го значения доходности для активов i, j;

N – число возможных значений доходности.

Понятие корреляции между доходностями активов аналогично понятию их ковариации. Корреляция доходностей активов i и j определяется как ковариация двух активов, деленная на произведение их стандартных отклонений.

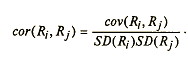
Существенного различия между терминами «корреляция» и «ковариация» нет. Деление ковариации на результат стандартного отклонения просто нормирует ковариацию, превращая ее в безразмерный показатель – коэффициент.

Коэффициент корреляции принимает значение в промежутке от -1 до +1. При этом значение, равное +1, отражает полное совпадение направления движения, а -1 означает полное несовпадение.

Таблица 1. Данные по корреляции 17 акций между собой

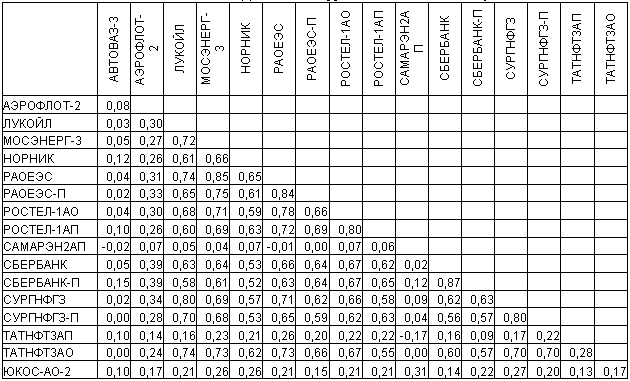
Интересные данные представлены в таблице 1, где показана взаимозависимость 17 акций торгуемы на ММВБ. Если присмотреться, то найдется всего несколько акций с отрицательной корреляцией. На их основе можно построить эффективные портфели Марковица.

В практике составления инвестиционного портфеля оценка ожидаемого значения, стандартного отклонения, ковариации и корреляции получается, исходя из статистических наблюдений за доходностью.

В общем виде вариация портфеля из G активов такова:

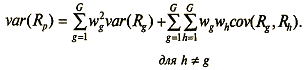
Поскольку вариация портфеля зависит от ковариации составляющих его ценных бумаг, несмотря на то, что риск отдельных активов может быть достаточно велик, риск самого портфеля можно снизить.

Технология создания эффективного портфеля из обширных групп ценных бумаг требует большого количества расчетов. Для портфеля из G акций требуется рассчитать (G2 – G)/2 ковариации. Поэтому для портфеля всего из 50 акций нужно подсчитать 1224 ковариации, а для 100 акций – 4950. Для нахождения портфелей с минимальным риском используются методы квадратичного программирования и соответствующее программное обеспечение. Обсуждение этих моделей выходит за рамки данной статьи. В нашем случае из 17 акций получится 136 ковариаций. Эффективные портфели из трех наиболее подходящих активов можно составить подбирая акции интуитивно. В результате получилось два инвестиционных портфеля. Они представлены в таблице 2.

Таблица 2. Эффективные инвестиционные портфели, составленные по теории Марковица

№	Портфели	Доходность	Риск
1	Самарэненого2ап-РАО ЕЭС об.-ТАТНЕФТп	6,41%	10,27%
2	Самарэнерго2ап-Автоваз-3-ТАТНЕФТп	7,66%	10,82%

При сопоставление данных рисунка 1 и таблицы 2 логично сделать вывод, что эффективные портфели Марковица обеспечивают высокую доходность при среднем риске. Оптимальный портфель, из указанных выше, пусть инвестор выберет самостоятельно.

Итак, основа стратегии диверсификации Марковица – это уровень ковариации доходностей активов портфеля. Заслуга Марковица в разработке инвестиционной теории состоит в постановке вопроса о риске активов как составляющих единого портфеля, а не отдельно взятых единиц.

Обсудить статью в форуме «Корпоративные финансы» >>>